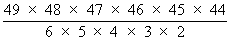Winning the Lottery
In the National Lottery, six ball are selected at random from 49 numbered balls. Players have to guess which six balls will be
drawn. If they get all six correct, they win the jackpot prize. We need to work out the total number of possible ways of choosing six different numbers from 49. Note that the order of
choosing the numbers does not matter.
There are 49 possible choices for the first ball.
For each of these 49 choices of the first ball, there are 48 possible
choices for the second ball (because one ball has already been taken
out)meaning there are 49 x 48 ways of choosing the first two balls.
However, because the order doesn't matter, this has to be divided by
2 (because the second ball can come before or after the first ball)

So the number of different possible choices for two balls can be written
as 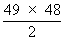 .
There are then 47 possible choices for the third ball, but since it
doesn't matter which position the third ball goes in
.
There are then 47 possible choices for the third ball, but since it
doesn't matter which position the third ball goes in

we divide by 3,
giving 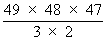 .
This sequence continues for all six balls which are chosen. So the total number of possible ways of choosing six balls from forty-nine is
.
This sequence continues for all six balls which are chosen. So the total number of possible ways of choosing six balls from forty-nine is 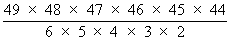
which is
equal to 13 983 816 or approximately 14 000 000 (14 million).
Therefore, the chance of a single ticket winning the jackpot is approximately one-in-14 million. Here is another way of looking at it:
If you attempt to guess one number chosen from 49 lottery balls then the probability that you are correct is 1/49. If you choose six numbers then the probability that one of them is the same as the first ball drawn is 6/49.
Because the first ball is not replaced, the probability for choosing the second ball is 1/48, but you have five chances, so the probability for drawing the second number correctly is 5/48.
The probability of choosing all six numbers correctly is:
6/49 x 5/48 x 4/47 x 3/46 x 2/45 x 1/44 = 1/13 983 816.
If your calculator has a button marked nCr you can get the answer directly.
nCr is shorthand for the number of different ways of choosing r items from n where the order does not matter.
"n" stands for the total number (here
n=49)
"r" stands for the number you want to select (here r=6)
So if you
type in the sequence 49 nCr 6 = you should get the result 13 983 816
directly.
Five winning numbers (bonus number not selected)
Since five of the six winning numbers must be picked, this means that one of the winning numbers must be excluded. There are six possibilities for the choice of excluded number, i.e. there are six ways for a pick of six to include exactly five of the six drawn numbers. The remaining number must be one of the 42 numbers left over after the six winning numbers and the bonus number have been excluded. Thus there are a total of 6 x 42 = 252 ways to have 5 out of 6 winning numbers. This becomes a probability of 252/13 983 816 = 0,00001802 or, equivalently, odds against of 55 490:1.
Four winning numbers
There are 15 ways to include four of the six winning numbers and 903 ways to include two of the 43 non-winning numbers for a total of 15 x 903 = 13 545 ways to have 4 out of 6 winning numbers, which works out to a probability of 13 545/13 983 816 = 0.0009686, that is odds against of 1 030:1.
Three winning numbers
There are 20 ways to include three of the six winning numbers and 12 341 ways to include three of the 43 non-winning numbers for a total of 20 x 12,341 = 246 820 ways to have 3 out of 6 winning numbers, which works out to a probability of 246 820/13 983 816 = 0,01765, that is odds against of 56:1.
Depending on your frame of reference (what is familiar to you), comparing the probability of winning at Lotto with the probability of tossing successive heads with a coin (the probability of getting n successive heads is 1/2n) may put it into perspective for you:
| Prize |
Odds against |
Equivalent number of successive heads |
| Jackpot (all 6 numbers correct) |
13 983 816 to 1 |
24 heads in a row |
| Third prize (5 numbers correct) |
55 490 to 1 |
16 heads in a row |
| Fifth prize (4 numbers correct) |
1 030 to 1 |
10 heads in a row |
| Seventh prize (3 numbers correct) |
56 to 1 |
6 heads in a row |

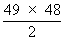 .
There are then 47 possible choices for the third ball, but since it
doesn't matter which position the third ball goes in
.
There are then 47 possible choices for the third ball, but since it
doesn't matter which position the third ball goes in
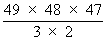 .
This sequence continues for all six balls which are chosen. So the total number of possible ways of choosing six balls from forty-nine is
.
This sequence continues for all six balls which are chosen. So the total number of possible ways of choosing six balls from forty-nine is