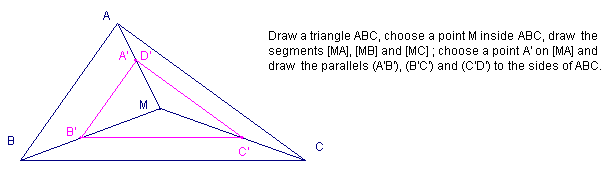
First reduce a triangle…
MAURICE STARCK
26 lot.Creugnet, Robinson 98810 MONT-DORE New-Caledonia
Theorem : If you cut a triangle, using a parallel to one side, so as to get a second triangle, then the two triangles have proportional sides.
This short presentation sets out to show how we can exploit this theorem in a research activity by analysing a diagram, proving the property which has been observed, generalising, asking oneself new questions, changing the point of view by moving from the plane to the space, then asking oneself more new questions.
1- In the plane

We observe that D’=A’, and to prove it we use the theorem three times in MAB, MBC and MCA (we get MA’=MD’).
And if we chose M outside the triangle (not on a side of ABC) ? The proof is still valid.
Will this reduction method work with a quadrilateral ? a non convex quadrilateral ? any polygon ? It does.
ABC has been reduced by cutting of along its sides three strips of different width.
Is it possible to choose M in order to have strips of same width ? M must lie on the bissectors, thus must be the centre of the inscribed circle.
And with a convex quadrilateral ? a convex polygon ? M must also be the centre of the inscribed circle… if it exists !
How to recognize such a quadrilateral ? Draw one around a circle and it becomes obvious that the sums of the lengths of the opposite sides must be equal.
Note : the circumscribed circle exist if the sums of the angles of the opposite sectors are equal (to 180°).
We know the ratio of the sides of the two triangles A’B’C’ and ABC : MA’/MA=k.
What is the ratio of their areas ? ABC is cut into three triangles with common vertex M ; using the theorem we prove that the ratio of the heights starting at M in MA’B’ and MAB is also k ; we deduce that the ratio of their areas is k2, and so for A’B’C’ and ABC. This proof works fine for any convex polygon, and also for non convex ones (with non crossed sides).
2- In the space
The first drawing shows a pyramid
(top view of a tetrahedron).
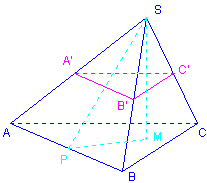
How to construct the template of such a pyramid ?
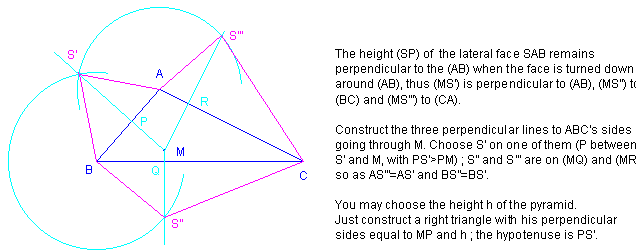
The construction works with M outside of ABC.
And with a quadrilateral base ? It works, even if the base is non convex, as it does with any non convex polygon with non crossed sides.
And what about A’B’C’ ? It is the section of the pyramid SABC by a plane parallel to ABC ; we have reduced the pyramid !
What is the ratio of the volumes of the two pyramids ? k3 of course (in SAM the theorem proves that the ratio of the heights is k).
Move the tehtrahedron, and you’ll find a view where the heights of the three trapeziums appear to be equal. What is the direction of that view ? the direction of (SI) where I is the centre of the circle inscribed in ABC.
"
Geometry is a skill of the eyes and the hands as well as of the mind. " (J.Pederson)
See also
http://www.ac-noumea.nc/maths/amc/polyhedr/tetra_.htm