The content and processes in the algebra strand in the grade 7-9 mathematics syllabus is based on two different, but related views on the nature of algebra, which give meaning and purpose to each item in the syllabus.

There are many situations involving two variables where the one variable is dependent on the other variable, i.e. where a change in the value of one (the independent) variable causes a deterministic change in the value of the other (the dependent) variable.

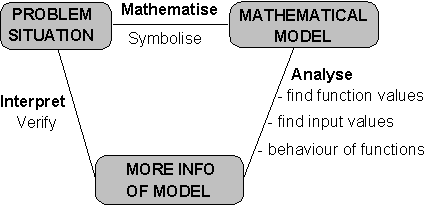
Algebra is a language and a tool to study the nature of the relationship between specific variables in a situation. The power of Algebra is that it provides us with models to describe and analyse such situations and that it provides us with the analytical tools to obtain additional, unknown information about the situation. We often need such information as a basis for reasoning about problematic situations and as a basis for decision-making. This view of algebra can be described as applied problem solving:

The main broad objectives of the algebra strand are

The mathematical model we construct of the situation may be represented in different ways: in words, as a table of values, as a graph or as a computational procedure (e.g. a flow diagram, expression or formula). The additional information we need to generate is mostly of the following three types:

1. finding values of the dependent variable (finding function values)
2. finding values of the independent variable (solving equations)
3. describing the behaviour of function values (increasing and decreasing functions, rate of change, gradient, derivative, maxima and minima, periodicity, . . .)

The additional information is obtained by different techniques in different representations of the model (e.g. finding function values by reading from a table, reading from a graph, or substituting into a formula). Some techniques are easier than others and/or yield more accurate results; Therefore, an important aspect of algebraic know-how is transforming from one representation of the model (e.g. a table) to another representation (e.g. a formula) which is more convenient to solve problems of the above three types. These transformations are summarised in the following diagram and table:

In particular, the above three problem types are handled more easily when a formula or function rule is available. Therefore finding formulae is important – it is our fourth problem type:

4. finding a function rule (formula)

Students should be able to find function rules in different representations of the model, i.e. to find the function rule from words, from a table or from a graph. The processes involved in finding function rules include induction (recognising a pattern in a table of values) and analytical processes (deduction, e.g. solving simultaneous equations). The relationships between tables, graphs and formulae are of particular importance (e.g. the relationship between a recursive common difference of 2 in a table, a gradient of 2 in the graph and the coefficient 2 in the formula y = 2x + 3).

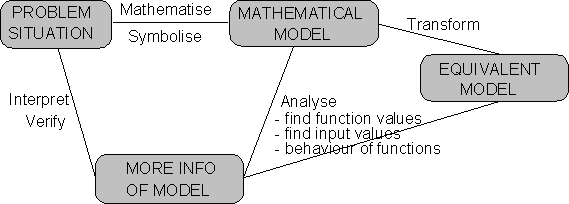
Sometimes the formula describing the relationship between variables may be "complex", making the first three problem types above very "complex". In such cases it is convenient to first transform the formula to an equivalent, but more convenient form for a specific task (from formula to formula in the previous table). This defines our fifth important problem type:

5. transforming to an equivalent formula ("manipulation" of algebraic expressions)

We make a few brief further remarks on equivalent transformations:

Algebraic manipulation is a useful tool in problem solving, but should not be elevated to a skill for its own sake. Therefore algebraic manipulation should be developed and practised in the context of equivalent transformations, as illustrated in the modelling diagram above. Our teaching should develop the meaning of equivalent expressions and students should experience the usefulness of such transformations to make the first three problem types above easier. For example, consider these two problems:

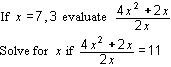
As they stand they are difficult. However, they become fairly easy once we transform
.

In problem solving, the choice of model depends on the properties of the model and the characteristics of the situation. In studying the relationship between variables, it is therefore important to analyse the different behaviours (i.e. properties) of different models (functions). In the junior secondary phase we study simple direct proportion (y = kx), the linear function (y = mx + c) and inverse proportion (xy = k), while quadratic, exponential, logarithmic and trigonometric functions are studied in the senior secondary phase.

It is important that the teaching programme provides for appropriate experiences of all the problem-types and that it develops the underlying concepts and techniques to enable students to experience the power of algebra as a tool to solve problems. However, it should be emphasised that our objective should be to solve problems, not to master isolated skills for its own sake (say factorisation).

The view that, historically, algebra grew out of arithmetic, and ought so to grow afresh for each individual, has much to say about the nature of Algebra and about the teaching and learning of Algebra. Algebra as generalised arithmetic generates "new" mathematical knowledge from existing mathematics through important mathematical processes such as induction, generalisation and proof.

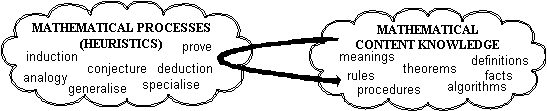
Algebra as generalised arithmetic can involve simple numerical situations such as investigating the sum of three consecutive numbers. An inductive approach (taking a number of special cases) may yield:

1 + 2 + 3 = 6

2 + 3 + 4 = 9

3 + 4 + 5 = 12

4 + 5 + 6 = 15

n + (n + 1) + (n + 2) = 3n + 1 =3(n + 1)

From this form, we should recognise that 3(n + 1) is a multiple of 3 for any value of. From this form we can also deduce that the sum is always three times the middle number.

Generalised arithmetic often deals with identities such as the one above. Algebra as a study of relationships between variables deals mostly with formulae. Both views of Algebra involve equations. Formulae, identities and equations are three different types of objects in algebra, defining different meanings of letter symbols as summarised below.