HANDLING PUPILS' MISCONCEPTIONS
Alwyn Olivier, Department of Didactics, University of Stellenbosch, Stellenbosch 7600
Presidential address delivered at the Thirteenth National Convention on Mathematics, Physical Science and Biology Education, Pretoria, 3 - 7 July 1989.
This paper will briefly delineate a theory for learning mathematics as a basis to reflect on (some particular) misconceptions of pupils in mathematics. Such a theory should enable us
1. THE ROLE OF THEORY
Teachers are often wary of theory - they want something practical. Yet, as Dewey has said, "in the end, there is nothing as practical as a good theory." How come? Theory is like a lens through which one views the facts; it influences what one sees and what one does not see. "Facts" can only be interpreted in terms of some theory. Without an appropriate theory, one cannot even state what the "facts" are. Let me illustrate with a story, taken from Davis (1984).
It is said that in Italy in the 1640's, the water table had receded so far that a very deep well had to be sunk in order to reach water. This was done. Then pumps were fitted to the pipes, and...disaster!...no water poured out of the spigot. It was clear that something was wrong, but what? Their understanding of the situation, i.e. their theory of pumping water, was that it was the pumps that pulled (sucked) the water to the surface. So the fault had to be with the pumps. New pumps were installed...better pumps were designed, built and installed...still no water. Then still better pumps, then even better ones. But the result was always the same: no water emerged from the spigot. They were baffled.
Finally, in 1643, Evangelista Torricelli, who invented the barometer, presented an alternative explanation (theory): It was not, he said, the pumps that pulled the water up. The pumps merely evacuated air from the pipes, creating unequal pressures at the two ends of the column of water, after which it was the atmospheric pressure that pushed the water up the pipes. This explained the difficulty: the air pressure is about 2,5 kg/cm, which is enough to support a column of water 10m high. It follows that if the water in a well is more than 10m deep, it cannot be pumped to the surface using atmospheric pumps. Building better and better atmospheric pumps would not resolve the issue - and that probably led to the invention of hydraulic pumps, which could do the job.
Let us again consider the role of theory. First, one cannot even discuss the matter without using some theory to explain the situation. Second, the objective fact that no water came out of the pumps, like the fact that a car refuses to start, does not lead anywhere. Unless you can say why there is no water, or why the car will not start, you are unable to do anything to change the situation. And in order to say why, you must interpret the "facts" in terms of an appropriate theory. Third, notice how the two different theories differed in their interpretation of the "facts" and suggested - prescribed! - different remedies to resolve the issue - one remedy was doomed, while the other offered some hope.
Now, has this story anything to say about the subject under discussion - pupils' misconceptions in mathematics? The fact is that our pupils often make mistakes in mathematics - don`t we know it! But unless we can say why they make these mistakes, we are unable to do something about it. And in order to say why, we must interpret these mistakes in terms of a theory - a learning theory. As teachers, all our interventions in the classroom are guided by some theory - be it conscious or subconscious - of how children learn mathematics. Different teachers hold different learning theories, and address pupils' mistakes in different ways. Could it be that all our frustrated efforts at eliminating errors are due to embracing an inappropriate learning theory - that we are trying to build better and better atmospheric pumps?
An escapist route, which is nevertheless a theory, is to view many pupils as rather dim, that they are not capable of understanding, and should rather not take mathematics. In general, it is not very useful to think of children's errors in terms of low intelligence, low mathematical aptitude, perceptual difficulties or learning disabilities. Of course these factors play a role, but if we are really concerned with helping individual children, such abstract ideas won't help - it is only when we work at the level of specific detail and get to know the specific roots of mistakes, that we are able to help.
The type of theory we adopt will also determine the importance of misconceptions for learning and teaching. Why should we care about pupils' misconceptions? What is the role of pupils' misconceptions in their learning? How will knowing what a pupil has got wrong help us to teach better?
2. LEARNING THEORY
I shall briefly outline two opposing learning theories, which will, by necessity, be both simple (presenting the ideas in oversimplified form) and simplistic (presenting the ideas in its most radical form), but which will illustrate different approaches to handling pupils' misconceptions.
2.1 Behaviourism
The behaviourist or connectionist theory of learning relates to an empiricist philosophy of science, that all knowledge originates in experience. The traditional empiricist motto is "There is nothing in the mind that was not first in the senses." Hence a person can obtain direct and absolute knowledge of any reality, because, through the senses, the image of that reality corresponds exactly with the reality (a replica or photo-copy).
Behaviourism therefore assumes that pupils learn what they are taught, or at least some subset of what they are taught, because it is assumed that knowledge can be transferred intact from one person to another. The pupil is viewed as a passive recipient of knowledge, an "empty vessel" to be filled, a blank sheet (tabula rasa) on which the teacher can write. Behaviourists, therefore, believe that knowledge is taken directly from experience, and that a pupil's current knowledge is unnecessary to learning.
This theory sees learning as conditioning, whereby specific responses are linked with specific stimuli. According to Thorndike's (1922) law of exercise, the more times a stimulus-induced response is elicited, the longer the learning (response) will be retained. The law of effect states that appropriate stimulus-response bonds are strengthened by success and reward (positive reinforcement) and inappropriate S-R bonds are weakened by failure (negative reinforcement). Consequently the organisation of learning must proceed from the simple to the complex, short sequences of small items of knowledge and exercise of these in turn through drill and practice. One learns by stockpiling, by accumulation of ideas (Bouvier, 1987).
From a behaviourist perspective, errors and misconceptions are not important, because it does not consider pupils' current concepts as relevant to learning. Errors and misconceptions are seen rather like a faulty byte in a computer's memory - if we don't like what is there, it can simply be erased or written over, by telling the pupil the correct view of the matter (Strike, 1983). This perspective is succinctly put by Gagne (1983: 15):
"The effects of incorrect rules of computation, as exhibited in faulty performance, can most readily be overcome by deliberate teaching of correct rules...This means that teachers would best ignore the incorrect performances and set about as directly as possible teaching the rules for correct ones."
2.2 Constructivism
A constructivist perspective on learning (e.g. Piaget, 1970; Skemp, 1979) assumes that concepts are not taken directly from experience, but that a person's ability to learn from and what he learns from an experience depends on the quality of the ideas that he is able to bring to that experience. This is again the same idea as our introduction about the role of theory: observation is driven by theory, so the quality of the observation is determined by the quality of the pre-existing theory. Knowledge does not simply arise from experience. Rather, it arises from the interaction between experience and our current knowledge structures.
The student is therefore not seen as passively receiving knowledge from the environment; it is not possible that knowledge can be transferred ready-made and intact from one person to another. Therefore, although instruction clearly affects what children learn, it does not determine it, because the child is an active participant in the construction of his own knowledge. This construction activity involves the interaction of a child’s existing ideas and new ideas, i.e. new ideas are interpreted and understood in the light of that child’s own current knowledge, built up out of his previous experience. Children do not only interpret knowledge, but they organise and structure this knowledge into large units of interrelated concepts. We shall call such a unit of interrelated ideas in the child`s mind a schema. Such schemas are valuable intellectual tools, stored in memory, and which can be retrieved and utilised. Learning then basically involves the interaction between a child’s schemas and new ideas. This interaction involves two interrelated processes:
(1) Assimilation: If some new, but recognisably familiar, idea is encountered, this new idea can be incorporated directly into an existing schema that is very much like the new idea, i.e. the idea is interpreted or re-cognised in terms of an existing (concept in a) schema. In this process the new idea contributes to our schemas by expanding existing concepts, and by forming new distinctions through differentiation.
(2) Accommodation: Sometimes a new idea may be quite different from existing schemas; we may have a schema which is relevant, but not adequate to assimilate the new idea. Then it is necessary to re-construct and re-organise our schema. Such re-construction leaves previous knowledge intact, as part or subset or special case of the new modified schema (i.e. previous knowledge is never erased).
Thus to understand an idea means to incorporate it into an appropriate existing schema. However, sometimes some new idea may be so different from any available schema, that it is impossible to link it to any existing schema, i.e. assimilation or accommodation is impossible. In such a case the learner creates a new "box" and tries to memorise the idea. This is rote learning: because it is not linked to any previous knowledge it is not understood; it is isolated knowledge, therefore it is difficult to remember. Such rote learning is the cause of many mistakes in mathematics as pupils try to recall partially remembered and distorted rules.
To the constructivist learning is not, as for the behaviourist, a matter of adding, of stockpiling new concepts to existing ones. Rather, learning leads to changes in our schemas.
It is clear that the character of a pupil's existing schemas will determine what he learns from experience or information and how it is understood. At the heart of a constructivist approach to teaching is an awareness of the interaction between a child's current schemas and learning experiences, to look at learning from the perspective of the child, for the teacher to put himself in the child's shoes, by considering the mental processes by which new knowledge is acquired. Because knowledge cannot be transferred ready-made, to support the child to construct his own knowledge, discussion, communication, reflection and negotiation are essential components of a constructivist approach to teaching.
From a constructivist perspective misconceptions are crucially important to learning and teaching, because misconceptions form part of a pupil's conceptual structure that will interact with new concepts, and influence new learning, mostly in a negative way, because misconceptions generate errors.
I distinguish between slips, errors and misconceptions. Slips are wrong answers due to processing; they are not systematic, but are sporadically carelessly made by both experts and novices; they are easily detected and are spontaneously corrected. I shall not consider slips in the rest of the paper. Errors are wrong answers due to planning; they are systematic in that they are applied regularly in the same circumstances. Errors are the symptoms of the underlying conceptual structures that are the cause of errors. It is these underlying beliefs and principles in the cognitive structure that are the cause of systematic conceptual errors that I shall call misconceptions.
If we want to account for pupils' misconceptions, we must look at pupils` current schemas and how they interact with each other, with instruction and with experience.
In order to reflect on some typical misconceptions of children, it will be useful to look a little closer at cognitive functioning. We would think of something like the following over-simplified process in cognitive functioning when a pupil tries to solve a problem (Davis, 1983):
1. Some item(s) of information in the problem is (are) selected to act as a cue to trigger the retrieval of a seemingly appropriate schema in the cognitive structure (memory).
2. Specific information from the problem ("values") are fed into appropriate "variables" in the retrieved schema. (If no values can be supplied, the schema will fill in values itself, from typical values in past experience. We call this a default evaluation.)
3. Some evaluative judgement of the suitability (the "goodness of fit") of steps 1 and 2 are made (and cycling back where necessary).
4. If the judgement is that steps 1 and 2 have been successful, the result (i.e. the combination of cue information from the problem and the content of the schema) is used to continue.
The process can be illustrated using the solution of the following equation:
x2 - 5x + 2 = 0
Step 1 consists of some visual cues in the equation - e.g. the exponent and the number of terms - that cause us to say (in effect): "Aha! It's a quadratic equation!", with the result that we retrieve from memory the "quadratic equation schema", which has many items of information, but which also (hopefully!) contains the quadratic formula:
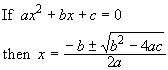
Step 2 involves looking at our specific problem x2
- 5x + 2 = 0 and taking from it certain specific information to enter into the "variables" of our memorised formula in the schema. We see that "1" should be used as a replacement for a, "- 5" for b and "2" for c.Step 3 involves whatever checks we carry out in order to convince ourselves that this is all correct, after which use of the quadratic formula (step 4) easily produces the answer.
A pupil can fail to solve the problem for many reasons, e.g. in step 1:
It is important to realise that once step 4 has been reached, the solution of the problem is wholly determined by the combined information of the used cues and the content and structure of the retrieved schema, e.g. if in our example above the quadratic formula in the schema (memory) was flawed, our solution would be flawed. We say the solution is mediated by the schema.
Let us now look at some specific misconceptions by analysing in what ways current schemas mediate new learning leading to misconceptions. One should acknowledge, of course, that errors are also a function of other variables in the education process, including the teacher, the curriculum, social factors, affective factors, emotional factors, motivation, attitudes, and possible interactions among these variables. For this paper, however, I shall concentrate only on cognitive variables.
3. SOME MISCONCEPTIONS AND THEIR GENESIS
3.1 Patchwork
What order of difficulty do we expect in the following three additions for young pupils learning column addition?
|
(A) |
523 |
(B) |
593 |
(C) |
586 |
(D) |
586 |
|
+25 |
+25 |
+25 |
+325 |
Traditional analysis would suggest that (A) should be the easiest, since (B) involves an extra "carry", (C) two "carries" and (D) involves an extra addition. Surprisingly, (A) is the most difficult for many children! Why should this be, and how do we account for the following frequent responses to (A)?
|
(E) |
523 |
(F) |
523 |
(G) |
523 |
|
+25 |
+25 |
+25 |
|||
|
748 |
948 |
48 |
Maybe we may diagnose that such pupils don't understand place-value, or don't understand "carrying", or that they don't know their number combinations, and we may remediate the problem by teaching these "missing concepts", or by teaching and reteaching the correct procedure directly.
Yet, clinical research (e.g. Davis, 1984) suggests that the "misconception" is elsewhere, and that these errors are quite plausible, as seen from the perspective of the child, whose response is mediated by his existing schemas based on previous learning. To solve (A), the addition cue triggers the child’s addition schema, which may include an item to add column by column, but may also include that addition is a binary operation - to add one needs two numbers. But in (A) there is an isolated digit, only one number! When the pupil is blocked in his progress, he does some patchwork: he distorts the column-by-column rule in order to satisfy the need for two numbers (E and F), or ignores the left-column (G) so as not to violate his notion of addition as a binary operation. This analysis also explains why many pupils are more successful in (B) than in (A). From this analysis it can also be expected that the same phenomenon will show itself in subtraction, and, indeed, it does (e.g. 276 - 14 = 162).
It is clear that successful remediation will build on the pupil's correct knowledge by introducing 0 as a placeholder in the isolated digit column, so that the child's addition schema is extended to reconcile the conflicting column-by-column and two-numbers rules. Direct teaching of the correct procedure, on the other hand, in no way eliminates the underlying cause of the erroneous behaviour and therefore does not change the schema. Although direct instruction may produce a change in performance, this change is often not permanent - before long the original schema reasserts itself, and the child's behaviour reverts back to what it was before instruction. (See also 3.6)
Pupils often degenerate into distorting rules to allow a schema to overcome some obstacle. Here is a high school example:
e + f = 8
Þ
e + f + g = ?
If a pupil's arithmetic addition schema is retrieved, it will require that numbers be added. Blocked in its progress because no values can be given for the letters, the schema will make a default evaluation and somehow manage to produce replacement numbers. In our research (Olivier, 1984), 58% of std 6 pupils supplied a numerical answer to the question. The most common responses were 12 (from 4 + 4 + 4), 15 (from 3 + 5 + 7, introducing a relationship between alphabetic order and number order) and 15 (from 8 + g, and g is the 7th letter of the alphabet!). This example again illustrates to what extent pupils' attack on a "new" problem is influenced by their attempts to relate it to previously learned ideas, or, put differently, to what extent previously learned ideas actually guide or direct their response to a "new" problem.
3.2 Ordering decimals
The following question is from a recent std 5 mathematics competition:
Which number is the largest?
|
(A) 0,62 |
(B) 0,234 |
(C) 0,4 |
(D) 0,31 |
(E) 0,532 |
Response:
|
0,62 |
(38%); |
0,532 |
(29%); |
0,4 |
(25%) |
Would we expect this result, and can we explain the errors and the sources of the errors?
Studies in Israel, the United States and France (Resnick et al, 1989; Nesher, 1987) have obtained similar results, and have shown that these errors are not slips, but that they are systematic errors based on children's pre-existing valid knowledge. What pre-existing knowledge is at stake and how does it interfere with pupils' attempts to order decimals?
First, pupils choosing 0,532 are using their valid knowledge of ordering whole numbers, e.g. "0,532 is bigger than 0,62 because 532 is bigger than 62, so the longest number is the biggest."
Second, pupils choosing 0,4 are using their valid knowledge of ordering common fractions, e.g. "0,4 is bigger than 0,62 because tenths are bigger than hundredths, so the shortest number is the biggest."
A child newly learning about decimals must build a schema of decimal numbers and relate it to previously acquired whole numbers, common fractions and measurement. This prior knowledge can support (there are many common features), but can also interfere (there are crucial differences) with the child’s construction of a correct and adequate schema for decimals. From results such as those illustrated above, it is only too clear that this prior knowledge is interfering with many children's decimal concepts. This can be attributed to an overgeneralization of the properties of whole numbers and common fractions to decimals, but mainly it means that pupils have not accommodated their previous schemas to include decimals; children view the new system of decimals as "identical" to the previous systems, ignoring the differences between the systems, i.e. they distort the concept of decimals so that it can conveniently be assimilated into existing schemas. Their decimal schemas are therefore inadequate and defective.
I argue, however, that although children may have a defective decimal schema, they manage to cope quite well in the school situation. It is exactly this success that works against any attempt at accommodation, because pupils realise full well that they can handle decimals with their previous conceptions, so why make the effort to change? No accommodation is necessary. I am, in effect, saying that our limited mathematical expectations of pupils are partly to blame for the omnipresence of these misconceptions. First, our teaching does not emphasise conceptual understanding of decimals, but rather emphasises algorithmic expertise. We are satisfied if pupils can add, subtract, multiply and divide decimals. The point is that these procedures are mainly taught by rules that reduce the operations to operations on whole numbers (e.g. to multiply two decimals, ignore the comma and multiply the whole numbers...). No conceptual understanding of decimals are required for such rules; no wonder pupils think they can manage with their whole number ideas. Second, pupils having the two misconceptions mentioned, will have a 100% success rate when initially comparing decimals of equal length, thus reinforcing their misconception, and neither they nor their teacher will realise that they are obtaining correct results with a defective strategy. Furthermore, if exercises are not intentionally designed to diagnose and discriminate such misconceptions (e.g. 0,4 vs. 0,32 will not discriminate the fraction rule and 0,4 vs. 0,62 will not discriminate the whole number rule), pupils may have a high success rate, believing their mistakes were mere slips. This identifies an important perspective on pupils' misconceptions, as explicated by Lèonard and Sackur-Grisvard (1987):
"Erroneous conceptions are so stable because they are not always incorrect. A conception that fails all the time cannot persist. It is because there is a local consistency and a local efficiency in a limited area, that those incorrect conceptions have stability." (p. 44)
"For what problems are those conceptions mathematically correct? For what problems are they erroneous? It is only when we know the mathematical limits of the student's misconception, that we will be able to know when their conceptions will fail, to prevent them, and eventually to teach them to students." (p. 45)
I mention two further interesting snippets from Resnick's research. Apparently the whole-number misconception declines with age, while the fraction misconception is more persistent and increases with age. Different curriculum sequences produce different misconceptions, as illustrated by the finding that French children by and large avoid the fraction misconception and outperformed children in Israel and the United States; in France decimals are taught before common fractions. This, of course, confirms that children's misconceptions derive from attempts to integrate new knowledge with already established knowledge.
3.3 Generalising over numbers
It is a well-known fact that pupils who have learned to solve quadratic equations by factoring, e.g.
x2 – 5x + 6 = 0
Þ (x – 3)(x – 2) = 0
so, either x - 3 = 0 or x - 2 = 0, tend to make the following error:
x2 – 10x + 21 = 12
Þ (x – 7)(x – 3) = 12
so, either x
- 7 = 12 or x - 3 = 12.This error is very difficult to eradicate - or is, at least, very difficult to eradicate permanently. Even with able pupils, receiving excellent instruction emphasising the special role of zero in the zero product principle, this error will continue to crop up in pupils’ work. Despite careful explanations of why it is an error and despite short-term elimination of the error, it keeps coming back. How do we explain it?
Matz (1980) presents a theory that explains the persistence of this error. There are two levels of procedures guiding cognitive functioning: surface level procedures, which are the ordinary rules of arithmetic and algebra, and deep level procedures
, which create, modify, control and in general guide the surface level procedures. One such deep level guiding principle is the generalisation over numbers, which, in effect says that "the specific numbers don't matter - you could use other numbers." This is a very important and in most cases a very necessary observation, which comes naturally to children, e.g. when learning to add, say 52 + 43 by column addition, a child will never master arithmetic if he believed the method works only for 52 + 43. He must believe that the method also works for 34 + 23 and 46 + 21 or any other sum than 52 + 43, also for combinations he has never seen before. Thus, in order to learn arithmetic a pupil must have such a deep level procedure generalising over numbers.This works very well; as a matter of fact too well: pupils have the natural tendency to overgeneralize over numbers. Because pupils are so accustomed to generalise over numbers, one can predict that errors will be made for any type of problem whose specific numerical values are critical. Overgeneralization of number and number properties may be the single most important underlying cause of pupil's misconceptions.
This is exactly what happens in the case of the quadratic equation. In (x – 3)(x – 2) = 0, the numbers 3 and 2 are not critical to the method, but the 0 is! Pupils should therefore generalise:
(x – a)(x – b) = 0
implies x – a = 0 or x – b = 0 (1)
Pupils who fail to realise the critical nature of the 0, treat it just as they do the other numbers and overgeneralize:
(x – a)(x – b) = c
implies x – a = c or x – b = c (2)
Equation (2) would be a correct generalisation of equation (1) if generalising were appropriate in this case. Unfortunately it is not. It is probably the first important rule pupils have met where some specific number should not be generalised.
We all know this. What is interesting, is our awareness of the guiding deep level procedure of generalising over number as the cause of the error; the surface level procedures are operating correctly. This explains why the error is so obstinate and resistant to change, despite our best efforts, and despite pupils' best intentions: it is not just a matter of learning, it cannot simply be erased from memory, because it is continually being re-created by a sensible deep level guiding principle. What is lacking is a critic - a danger signal that in this particular case the application of the deep level procedure is wrong, which probably only comes with experience of making such mistakes.
This example shows again the sensibility of pupils' errors and how pupils' misconceptions are not random, but originate in a consistent conceptual framework based on earlier acquired knowledge.
3.4 Generalising over operations
If you teach mathematics in primary school and probably even if you teach in high school, you will recognise the following as a frequent and persistent error (Van Lehn, 1982):
|
263 |
546 |
|
– 128 |
– 375 |
|
145 |
231 |
To remediate the error one may try direct teaching of the correct algorithm and address issues such as place-value, "borrowing" and number combinations. Yet we all know that this error is extremely obstinate and resistant to change - it will recur again and again.
Are our diagnoses correct? If we want to account for pupils' systematic errors from a constructivist perspective, analysing the procedures and their prerequisites is not sufficient. We must, especially, know how this new knowledge is embedded in a larger meaning system that the child already holds and from which he derives his guiding principles; we must analyse what knowledge in previous learning may be influencing a new idea.
Available research (e.g. Davis, 1984) suggests that one guiding principle is children’s erroneous conception that subtraction is commutative, i.e. the order does not matter, so 6 - 4 and 4 - 6 are the same, or rather they have the same answer.
Why would pupils think that subtraction is commutative? Again, it is an outcome of their experience influenced by correct previous learning. In the system of whole numbers in primary school children work only with 6 – 4; 4 – 6 only arises when we introduce negative numbers in std 6, so the need to discriminate between the two forms never really arises. We also know that children – and humans in general - generally do not discriminate any finer than is needed in a given situation, i.e. discriminations are not made where they are not presently needed (Davis, 1984).
The commutativity of subtraction is further reinforced by word problems containing phrases such as "the difference between Bill's age and Mary’s age is 2 years", without specifying who is older, so presumably 6 - 4 and 4 - 6 both produce 2 as result (actually, this is an early conception of absolute value!). Also, have pupils not often heard to always "take the smaller from the larger", which is exactly what they are doing in the beginning examples? The point is that although children know 6 – 4 and 4 – 6 have different meanings, they may reason that the method to get the answer of 4 – 6 is to calculate 6 – 4, which is the only physical meaning they have available; so 6 – 4 and 4 – 6 are, by definition, equal in value. Even high school teachers will frequently find that pupils write (300 + 400) – 1800 for an angle in a triangle, but calculate 700 – 1800 = 1100.
But the main contributory influence for seeing subtraction as commutative is probably that pupils have extensive experience of the commutativity of addition and multiplication when learning their tables, and, in lieu of any contradictory evidence, they have no reason to expect that subtraction will behave otherwise. They are overgeneralizing over operations. We can predict that the same misconception will show itself in division, and, indeed, it often does (although other misconceptions are induced by the intuitive meanings of the operations - see next paragraph). It is possible that the early introduction of calculators in the primary school may alleviate this particular misconception.
One of the largest and most frequently occurring class of errors in the high school, which Matz (1980) calls linear extrapolation errors, is illustrated by the following examples:
Ö (a + b) = Ö a + Ö b
I shall not delve into the problem here, except to say that these errors are probably grounded in an overgeneralization of the "distributive property", which children encounter often in arithmetic and in introductory algebra, and where it is natural to work with each part independently, e.g.
a(b + c) = ab + bc
a(b – c) = ab – ac
![]()
(ab)n = an bn
![]()
Putting it differently, these errors are an overgeneralization of the property f(a + b) = f(a) + f(b), which applies only when f is a linear function, to the form f(a * b) = f(a) * f(b), where f is any function and * any operation. This super-formula now acts as another deep level procedure, saying "work the parts separately", so that the indicated errors are continually being re-created, which explains its obstinate recurrence.
As mentioned before, the error will probably only be resolved if the pupil develops (from experience of errors!) a critic that will recognize the deep level construction as an error. In this regard it is important to be aware of the conditions under which the deep level procedure may be applied.
3.5 Meanings
The following two problems differ markedly in difficulty to pupils (Bell et al, 1981; 1984). Why should this be? Can we predict and explain the difficulty?
(A) 1 liter of petrol costs R1,12. How much will it cost to fill a tank holding 3 liters?
(B) 1 liter of petrol costs R1,12. How much will it cost to fill a small tank which holds 0,53 liters?
Would we be surprised at a success rate of 27% for 13-year-olds for (B)? Ah, we would say, it is because pupils find decimals difficult! This explains nothing. What is it about decimals that pupils find difficult? Note that pupils were not required to perform the actual calculation, but only to indicate what operation was needed to solve the problem. So the difficulty does not lie in the calculation, but in the choice of operation. In Bell's study, 63% of pupils erroneously chose division in (B). Can we explain that?
The mediating or driving misconception causing the error is that "multiplication makes bigger and division makes smaller". So in (B) pupils reasoned that 0,53l is less that 1l, so it should cost less than R1,12. So to make it smaller they are driven by their misconception to choose division as operation.
What are the origins, the roots of these misconceptions? Well, as you have come to expect at this stage - in experience of successful previous learning. When working with whole numbers, multiplication always makes bigger (except for 0 and 1, which may be discarded as special cases). So it is, again, a case of an overgeneralization from whole numbers (where it is true) to decimal numbers (and probably fractions and integers, where it is not generally true).
The question is: why do pupils not make the necessary accommodation after working with fractions and decimals for some time; why do they not notice that it is not valid for decimals and fractions? The answer probably lies in our emphasis on the procedures for the operations, where any checking is done, not by estimation, but by repeating the same process. We therefore never focus our attention on the relative sizes of the factors and product in the multiplication of decimals. The misconception has no apparent detrimental effect on calculation, so we may not even notice it or be overly concerned about it. So the misconception is alive and well and influencing children's problem solving!
But the roots of the misconception lies deeper. Consider the following two problems used by Fischbein et al (1985):
(A) From 1 quintal of wheat you get 0,75 quintal of flour. How much flour do you get from 15 quintals of wheat?
(B) 1 kg of a detergent is used in making 15 kg of soap. How much soap can be made from 0,75 kg of detergent?
The numbers in both problems are the same, yet (A) yielded 79% success and (B) only 27% (with 45% choosing division). How can that be explained? The difference can be ascribed to pupils' implicit intuitive meaning of multiplication, namely repeated addition. In the repeated addition model of multiplication, multiplication necessarily makes bigger:
3
´ 5 = 5 + 5 + 5and multiplication is not commutative (or rather, the forms have different meanings):
5
´ 3 = 3 + 3 + 3 + 3 + 3In a repeated multiplication model 3
´ 0,47 has a meaning, but 0,47 ´ 3 cannot be interpreted as repeated addition. Now notice that in (A) the model is 15 ´ 0,75, which can be understood as repeated addition and therefore cannot be related to pupils' intuitive meaning of multiplication. It is clear that pupils'choice of operation is mediated by their original implicit model of multiplication.It is again clear that senior pupils have not progressed, have not accommodated their understanding of the meaning of multiplication beyond their first ideas. To be able to cope with area of a rectangle, and problems relating to speed, price, etc. the meaning of multiplication must be extended to include other models of multiplication, e.g. the idea of rate. Do we try to teach it at all?
Here is an example where children's interpretation of the meaning of symbols lead them astray:
"In a certain college there are six times as many students as there are professors. Use S for the number of students and P for the numbers of professors to write an equation for the situation."
In our research (Olivier, 1984), 58% of std 8 pupils erroneously responded with P = 6S, which means they are interpreting S as an abbreviation for "students" and P for "professors". In essence, they are using letter symbols as labels, or as abbreviations for units as in 6 gram = 6 g, which is probably children's first encounter with letter symbols. Pupils often carry this prior meaning into algebra, with disastrous results, as the example shows. This misconception of the meaning of letter symbols in algebra is reinforced when we treat 2x + 3x as mere abstract "letters" and a + b as apples and bananas. Pupils need to construct meaning for letters as numerical variables in order to cope with algebra.
3.6 Interference
Davis (1984) offers an alternative explanation for the students-professors error. He suggests that pupils may indeed have a numerical-variable schema available. But a schema such as the letter-as-label, which is acquired early and developed well may prove to be extremely persistent, so much that it may sometimes continue to be retrieved inappropriately long after one has become fully cognisant of the conditions under which it is or is not used. Put differently: a new appropriate schema may be available, but the old schema continues to exist. The source of such misconceptions lies in retrieving the wrong schema and not recognising the retrieval error. As for remediating the misconception, Davis advocates making sure that pupils are aware of both schemas and of the likelihood of incorrect choice.
This issue of the retrieval of an inappropriate schema is further illustrated by the following well-known teacher-pupil dialogue:
Teacher: What is four times four?
Pupil: Eight
Teacher: How much is four plus four?
Pupil: Oh! It should be sixteen!
How is this sequence to be explained? The addition schema is constructed first and is well developed. Thus, when a question is asked about multiplication, which is a more recent (and maybe less secure) piece of learning, the pupil replaces it with a question dealing with earlier (and presumably more securely learned) material. This replacement is also common in other cases, and we notice that it is nearly always the case that the replacement is with an earlier idea:
4
´ 4 becomes 4 + 4We notice also that the visual cues for the pairs of questions are very similar in nature. Maybe pupils are not discriminating the visual cues?
However, it is not always the case that previously learned skills interfere with new skills, but often also the other way around, e.g. x + x = 2x until pupils learn multiplication, then x + x suddenly becomes x2 .
Byers and Erlwanger (1985) suggest that this confusion should be sought in memory transformations and subjective organisation during retention. They suggest that many errors are due to attempts by students to simplify mathematical material. The student tries to introduce his own unity, coherence and consistency into material he has learned at different times, and to do so on the basis of hypotheses which appear to him to be both simple and sensible. Because in the event old and new concepts, strategies and algorithms tend to be confused and substituted for each other, the resulting errors are usually ascribed to "interference".
Jerome Bruner has also noticed this confusion:
"...when children give wrong numbers it is not so often that they are wrong, as that they are answering a different question. The teacher’s job is to find out what question they are in fact answering".
Teachers must help pupils to differentiate between such cases and stress the conditions under which each is applicable.
4. DISCUSSION
(1). The most essential message of this paper is that we should have sympathy - more: empathy, with children for their errors and misconceptions in mathematics. If we understand the general principles of cognitive functioning from a constructivist perspective, we will realise that, for the most part, children do not make mistakes because they are stupid - their mistakes are rational and meaningful efforts to cope with mathematics. These mistakes are derivations from what they have been taught. Of course, these derivations are objectively illogical and wrong, but, psychologically, from the child's perspective, they make a lot of sense (Ginsburg, 1977).
(2). We would probably all agree that mathematics is a cumulative subject, and that any new learning depends on previous learning. We would also agree that
* correct new learning depends on previous correct learning,
and also that
* incorrect new learning is often the result of previous incorrect learning.
What I have tried to show, is that
* incorrect new learning is mostly the result of previous correct learning.
Every misconception we have discussed had a legitimate origin in previous correct learning
- each misconception was correct for some earlier task, as performed in some earlier domain of the curriculum.(3). The source of misconceptions is mostly an overgeneralization of previous knowledge (that was correct in an earlier domain), to an extended domain (where it is not valid).
(4). A schema acquired early and developed well is highly resistant to change.
(5). Children do not easily accommodate new ideas when necessary, i.e. change their present schemas, but rather assimilate new ideas into existing schemas, which means that the new idea must to a certain extent be distorted to be "like" a previous idea.
(6). Traditionally, the university blames the high school for poor teaching, the high school blames senior primary, who blames junior primary, who blames the home...In our examples of misconceptions we have seen that pupils' early learning is correct, but that it is exactly this correct learning that is eventually the source of later misconceptions. Where does the problem really lie? Either earlier learning must be changed so that pupils' ideas will not later have to be changed (i.e. teach the "correct" notion from the start), or we must later make a special effort to prevent or remediate children's misconceptions. Neither is easy. For early learning, take "multiplication makes bigger" as an example, which we have shown, originates from the early teaching of multiplication as repeated addition. This leaves us with a fundamental didactical dilemma. If we continue to introduce multiplication via repeated addition, we create a strong, and resistant, but incomplete meaning of multiplication that will come to conflict with later meanings of multiplication. On the other hand, repeated addition is probably the best introductory meaning available for multiplication, so we have little choice but to continue in this way. The notion of decimals before fractions is an interesting possibility. But it is not possible to teach decimals before whole numbers, or algebra before arithmetic! There is little to change, we must accept the possibility that early learning may, through overgeneralization, lead to misconceptions.
Can we prevent or remediate misconceptions later? Yes and no. Yes, later teaching is presently not adequately aware of the major cognitive leaps pupils must make in e.g. the transition from whole numbers to decimals and fractions, and from arithmetic to algebra. Our later teaching emphasises computational and manipulative dexterity at symbolic level, rather than conceptual understanding. This dexterity does not require pupils to accommodate their existing schemas - many pupils` misconceptions are masked by adequate performance in mathematics. So, if later teaching really addressed the issues, we could prevent or remediate the mentioned misconceptions by helping pupils to integrate the new and the previous knowledge. No, because misconceptions may develop naturally as a product of typical human mental processing. Research shows that the initial intuitive ideas become so deeply rooted in the child's mind that they continue to exert an unconscious control over mental behaviour even after the child has acquired formal mathematical notions of the idea that are solid and correct (e.g. Fischbein et al, 1985).
(7). From a constructivist perspective the teacher cannot transmit knowledge ready-made and intact to the pupil. Errors and misconceptions are seen as the natural result of children's efforts to construct their own knowledge, and these misconceptions are intelligent constructions based on correct or incomplete (but not wrong) previous knowledge. Misconceptions, therefore, cannot be avoided. Such errors and misconceptions should not be treated as terrible things to be uprooted, since this may confuse the child and shake his confidence in his previous knowledge. Instead, making errors is best regarded as part of the process of learning. We should create a classroom atmosphere that is tolerant of errors and misconceptions and exploit them as opportunities to enhance learning. In this regard direct teaching ("telling") of missing concepts will not do. Rather teachers should help pupils to connect new knowledge to previous learning. Swan (1983), Nesher (1987) and Olivier (1988) describe a teaching approach that is designed to expose children's misconceptions and provide a feedback mechanism that leads to cognitive conflict. Discussion, communication, reflection, and negotiation of meaning are essential features of a successful approach to resolve pupils' misconceptions.
REFERENCES
Bell, A., Fischbein, E. & Greer, B. (1984). Choice of Operation in Verbal Arithmetic Problems: The Effect of Number Size, Problem Structure and Context. Educational Studies in Mathematics 15: 129-147.
Bell, A., Swan, M. & Taylor, G. (1981). Choice of Operations in Verbal Problems with Decimal Numbers. Educational Studies in Mathematics 12: 399-420.
Bouvier, A. (1987). The Right to Make Mistakes. For the Learning of Mathematics 7,3: 17-25.
Byers, V., & Erlwanger, S. (1985). Memory in Mathematical Understanding. Educational Studies in Mathematics 16: 259-281.
Davis, R.B. (1983). Complex Mathematical Cognition. In H.P. Ginsburg (Ed.). The Development of Mathematical Thinking (pp. 254-290). Orlando, Florida, Academic Press, Inc.
Davis, R.B. (1984). Learning Mathematics. The Cognitive Science Approach to Mathematics Education. London. Croom Helm.
Fischbein, E., Deri, M., Sainati, N. & Marino, M.S. (1985). The Role of Implicit Models in Solving Verbal Problems in Multiplication and Division. Journal for Research in Mathematics Education 16: 3-18.
Gagne, R.M. (1983). Some Issues in the Psychology of Mathematics Instruction. Journal for Research in Mathematics Education 14: 7-18.
Ginsburg, H. (1977). Children`s Arithmetic: The Learning Process. New York. D. Van Nostrand Company.
Lèonard, F. & Sackur-Grisvard, C. (1987). Necessity of a Triple Approach of Erroneous Conceptions of Students, Example of the Teaching of Relative Numbers. (1) Theoretical Analysis. In J.C. Bergeron et al (Ed.). Proceedings of the Eleventh International Conference for the Psychology of Mathematics Education (Vol II)(pp. 444-448). Montreal.
Matz, M. (1980). Towards a Computational Theory of Algebraic Competence. Journal of Mathematical Behaviour 3,1: 93-166.
Nesher, P. (1987). Towards an Instructional Theory: The Role of Student`s Misconceptions. For the Learning of Mathematics 7,3: 33-40.
Olivier, A.I. (1984). Introductory Algebra. In-Service Education Course, Cape Education Department.
Olivier, A.I. (1988). The Construction of an Algebraic Concept through Conflict. In A. Borbas (Ed.). Proceedings of the Twelfth International Conference for the Psychology of Mathematics Education (pp. 511-518). Veszprem, Hungary.
Piaget, J. (1970). Genetic Epistemology. Chicago. University of Chicago Press.
Resnick, L.B., Nesher, P., Lèonard, F., Magone, M., Omanson, S. & Peled, I. (1989). Conceptual Bases of Arithmetic Errors: The Case of Decimal Fractions. Journal for Research in Mathematics Education 20: 8-27.
Skemp, R.R. (1979). Intelligence, Learning and Action. New York. John Wiley & Sons.
Strike, K. A. (1983). Misconceptions and Conceptual Change: Philosophical Reflections on the Research Program. In H.Helm and J.Novak (Eds). Proceedings of the International Seminar on Misconceptions in Science and Mathematics (pp 85-97). Ithaca, Cornell University.
Swan, M. (1983). Teaching Decimal Place Value. A Comparative Study of "Conflict" and "Positive Only" Approaches. In R. Hershkowitz (Ed.). Proceedings of the Seventh International Conference for the Psychology of Mathematics Education (pp. 211-216). Rehovot, Israel. Weizmann Institute of Science.
Thorndike, E. (1922). The Psychology of Arithmetic. New York. Macmillan.
Van Lehn, K. (1982). Bugs are not Enough: Empirical Studies of Bugs, Impasses and Repairs in Procedural Skills. Journal of Mathematical Behaviour 3,2: 3-71.