Frames:

8. Constructing coordinate proofs

Descartes intended the analytical method as a way to discover new theorems in Geometry. The method of Coordinate Geometry also provides an interesting alternative to prove conjectures and solve problems in Synthetic Geometry.

The most important step in starting a proof is to place your figures on the coordinate plane, in such a way that proofs are then simply derived, while taking care not to fall into the trap of using special cases leading to invalid deductions.

Guidelines for placing figures on a coordinate plane:
1.  Place a vertex or centre at the origin.
2.  Place at least one side of a polygon on an axis.
3.  Keep the figure within the first quadrant, if possible.
4.  Use coordinates that make calculations as simple as possible.


Use Coordinate Geometry to prove:

If the diagonals of a parallelogram are equal, then the parallelogram is a rectangle.

Click for a discussion:
Sorry, this page requires a Java-compatible web browser.

ABCD is a parallelogram, with vertices A(-1, 4), B(3, 6) and D(4, 1). Find the coordinates of C.
Try to solve it in more than one way.

Click here for a discussion:  

Concurrency
Let’s now return to the work on concurrency we did in Unit 2 on Synthetic Geometry, but now look at some results from an Analytic Geometry point of view.


Open the Circumcentre applet:     

ΔABC is has vertices A(3, 8), B(1, 2) and C(9, 2).

  1. Prove that the perpendicular bisectors of the three sides are concurrent, i.e. meet in one point (P), and calculate the coordinates of this point (the circumcentre).
  2. Prove by calculation that P is equidistant from A, B and C.
  3. Find the equation of the circumscribed circle of ΔABC.
  4. Find the locus of P:
    a. if B and C are fixed and A is variable (drag point A to see the locus).
    b. if B and A are fixed and C is variable (drag point C).
    c. if A and C are fixed and A is variable (drag point B).

Open the Centroid applet:   

ΔABC has vertices A(3, 8), B(1, 2) and C(9, 2).

  1. Prove that the medians of the three sides of this triangle are concurrent, i.e. meet in one point (P), and calculate the coordinates of this point (the centroid).
  2. Prove by calculation that AP:PN = 2:1
  3. Find the locus of P if vertex A moves along the horizontal line RS (drag or animate A).
    What if BC is not horizontal (drag B or C)? What is then the locus?
    What if RS is not horizontal (drag R or S)? What is then the locus?
    Prove your conjectures!
  4. Prove, in general, that if the coordinates of A, B and C are (x1,  y1), (x2,  y2) and (x3,  y3) respectively, the coordinates of the centroid is given by the formula
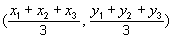
Click here for the solution:   

Open the Orthocentre applet:  

If we think of the vertices of a triangle as variables, then as the vertices move, so will the orthocentre. But how does it move, what is its locus?
  1. Can you visualise what path P will follow if B moves along the red line?
    Now drag or animate point B ...
    Surprised? Prove that the locus is a parabola and find its equation.
  2. Click Locus 2 to change the red line and clear traces.
    What is now the locus of P if B moves along the red line? Surprised? Can you prove it?
  3. Now click Locus 3 and clear traces.
    What is the locus of P if B moves along the red circle? Can you prove it?
Click here for the solution:  

We should follow the Descartes philosophy:
Doubt everything and accept nothing as true except that which you recognizes as clearly such!

How convinced are you about the above guidelines for placing figures on a coordinate plane?
How can such a placement give us a valid general proof for any shape and any location of the figure, when we use special figures with special properties and assume special locations (positions)?

Describe at least two examples where too special placement of a figure on the coordinate axes can lead to mistakes.