1.
Introduction
It is important to know the different specific formulae and shapes of
the basic function types, i.e. linear, quadratic, cubic, absolute function,
exponential, logarithmic, trigonometric, …
This unit emphasizes the importance
of understanding the similarities across all these different function
types, i.e. that we generalise the transformations of functions across
all these different functions.
This allows us to
draw the graph of any function in exactly the same way through transformation
of the basic function forms like
y
= x,
y
= x2, etc. This means that the common structure in the formulae of the following functions also leads to a common structure in their graphs:
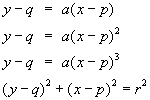 |
What is common in the formulae of these functions?
What is common in the graphs of these functions? | |
Using the structure
of functions in this way is empowering – instead of trying to remember
and reproduce the behaviour of many different types of graphs, they can
easily be reconstructed through a few simple transformation rules.
This unit aims at
giving you different experiences, especially through various technology
media, to develop and reinforce your understanding of the transformations
of functions.
|
Outcomes |
|
After
working through this unit you should be able to:
- Identify
and use various kinds of symmetry in functions, numerically,
graphically and algebraically.
- Identify
and use horizontal and vertical translations, i.e. transformations
of the type
f(x
– k) and f(x)
+ k.
- Identify
and use horizontal and vertical scaling of graphs, i.e.
transformations of the type
kf(x)
and f(kx).
- Understand
the influence of parameters on the behaviour of graphs.
- Use
algebraic transformations to draw graphs.
|
|
|