Investigating theorems
As teachers
we know that learners find it difficult to remember their theorems. Maybe
we should try a different strategy! Let the learners rather investigate and formulate conjectures for themselves before
they try to prove it. This will mean that they will not just be learning
the theorems by heart, but will learn with understanding.
Let’s now investigate
the proportionality theorems ourselves!
Proportionality
theorems
In
the applet, drag point D. What do you observe?
Now change the triangle, then move D again. What do you observe?
Can you formulate a conjecture?
Note: What happens if D moves beyond A on BA extended?
Also formulate the converse
for your conjecture.
|
|
Proportionality
theorems
If a line is parallel to one side of a triangle, then it divides the other
two sides proportionally.
If a line divides
two sides of a triangle proportionally, then it is parallel
to the third side.
|
|
Towards
a proof
In
the applet, drag the red points. What do you observe? How can these ideas
help in proving the two proportionality theorems?
Can
you give reasons for each step of this proof?
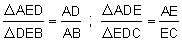
But DDEB = DEDC
Therefore 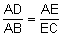
Specialise
How is the Grade 10 “midpoint theorems” a special case of
the proportionality theorems?
Generalise
In the applet, in trapezium ABCD, PQ || AD || BC.
Prove that PQ
divides AB and CD proportionally.
How is this a generalisation
of the triangle proportionality theorem?
|
|
|
Generalise
The
applet shows three parallel lines. Move C’ or A’ —
what do you notice?
Now move B — what do you notice?
Now move point A down. What do you notice?
Can you formulate a conjecture?
How is this a generalisation of
the triangle proportionality theorem?
Can you prove
it?
|
|
|