2.
The history of Analytical Geometry
2.1.
René Descartes
 |
“I
am thinking, therefore I exist.” or “I think, therefore
I am.”
(Latin: Cogito ergo sum)
René Descartes: Discours de la Méthode, 1637 “Each
problem that I solved became a rule which served afterwards to solve
other problems.”
René Descartes: Discours de la Méthode, 1637 |
René Descartes
(1596-1650) is generally regarded as the father of Analytical Geometry .
His name in Latin is Renatius Cartesius — so you can see
that our terminology “Cartesian plane” and “Cartesian
coordinate system” are derived from his name! Analytical Geometry
is also often called Cartesian Geometry or Coordinate geometry.
Descartes is also generally regarded
as the father of modern philosophy. His life spanned one of the greatest
intellectual periods in the history of all civilization. To mention only
a few of the giants: Fermat and Pascal were his contemporaries in mathematics.
Shakespeare died when Descartes was twenty, Descartes outlived Galileo by
eight years, and Newton was eight when Descartes died. Descartes
is so famous that the town in France where he was born — La Haye —
has been renamed to Descartes. His face has been on many stamps throughout
the world.
Descartes believed
that a system of knowledge should start from first principles and proceed
mathematically to a series of deductions, reducing physics to mathematics.
In his Discours de la Méthode (1637) — the full
title was “Discourse on the Method of Rightly Conducting the Reason
and Seeking Truth in the Sciences” — he advocated the systematic
doubting of knowledge, believing as Plato that sense perception and reason
deceive us and that man cannot have real knowledge of nature. The only
thing that he believed he could be certain of was that he was doubting,
leading to his famous phrase "Cogito ergo sum", (I think, therefore
I am). From this one phrase, he derived the rest of his philosophy.
Descartes formulates
the following principles for the reasoning process:
- accept nothing
as true except that which you recognize as clearly such;
- divide each difficulty
that you meet into manageable pieces;
- proceed in your
thinking, stage by stage, from the simple to the complex;
- review your thinking
carefully to ensure that nothing has been omitted.
Descartes showed that
if a geometric construction requires in its analytic form nothing but
addition, subtraction, multiplication, division, and the extraction of
square roots, then it can be achieved with ruler and compass. These arithmetic
operations are to be applied to the two coordinates of each point given
by the construction problem. Conversely if it can be achieved with ruler
and compass, then when represented analytically all points involved in
the construction will have coordinates that can be obtained from those
of the points initially given by these five arithmetic operations. The
results may be very complicated, for example, if (a; b) and (c; d) are
two of the points given, one new coordinate might be
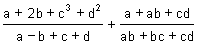
This point reached,
we can now concentrate almost entirely on the algebra!
|