6.
More circle loci
The
mathematical attitude always tries to generalise problems!
In the previous
section we found the locus of the midpoint of a chord AB of a circle.
Let’s now generalise: What if B is not a point
on the circle, but any point in the plane?
|
If B
is a fixed point in the plane and A is any point on circle
M, what is the locus of P, the midpoint of segment AB for all
positions of A on the circle?
First try to visualise it and formulate a conjecture.
Check your conjecture by dragging or animating A in the applet. Then move B and M to different positions and
repeat.
Use Synthetic Geometry to prove that the locus of P is a
circle. Where is it’s centre and what is it’s radius?
|
|
|
Not so easy this time? Then let’s try an Analytical Geometry
approach!
Let’s place the information conveniently on a coordinate system,
and reflect on what general conclusions we can draw from our placements.
First,
let’s investigate simple special cases: place B at the origin, and let M be any point
on the X-axis.
Move (drag) or animate point A. How will you describe
the locus of P? Then vary M, clear traces, and animate again.
Choose
appropriate coordinates for A, M and P
and deduce the equation and description of the locus of P.
Is this the solution of our original problem?
|
|
Click
here for the solution: 
|
|
|
Now look at a more general case:
Keep B at the origin, but let M be
any point in the plane.
Move (drag) or animate
point A. How will you describe the locus of P? Then vary M, clear traces, and animate again.
Choose
appropriate coordinates for A, M and P and deduce the equation
and description of the locus of P.
|
|
Click
here for the solution: 
|
|
|
Let’s
now look at the general case:
Let B and M be any points on
the plane.
Move (drag) or animate point A.
How will you describe the locus of P?
Choose
appropriate coordinates for A, B, M and P and deduce the equation
and description of the locus of P. Comment on the validy and convenience of
the different placements of the information on the coordinate system.
|
|
Click
here for the solution: 
|
|
|
Comment:
Because
our applet in Locus Segment 1 is a special case, we can easily be misled
visually to think that the centre of the locus circle lies on
the X-axis or even that the centre lies on circle M, but that is not the
case: move point M and animate again ….
We can easily make
the same mistake in our interpretation of the above algebra! But if we
do not interpret that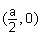 
is on the X-axis, but merely that it is the midpoint of segment BM, then the placement
and our conclusions in Locus Segment 1 are completely valid!
All three placements
and proofs are quite valid and general. It is therefore more convenient
to use the simplest placement and coordinates in Locus Segment 1 without loss of generality, because it makes the
mathematical manipulation so much easier … Do you agree on both statements, i.e. the special placement is general, and the special placement simplifies the proof?
Let’s now return to our question at the top of the page:
B
is a fixed point in the plane and A is any point on circle
M. Use Synthetic Geometry to prove that the locus of P, the midpoint of segment AB is a circle for all
positions of A on the circle.
Where is it’s centre and what is it’s radius?
Click
here for answer: 
|
|
|
|
|