1. Introduction

Studying the conics provides us with a context to further develop our understanding of the Analytical Geometry method, integrating Geometry and Algebra, and to re-visit our understanding of the content of the parabola and the hyperbola by seeing them in a new light.

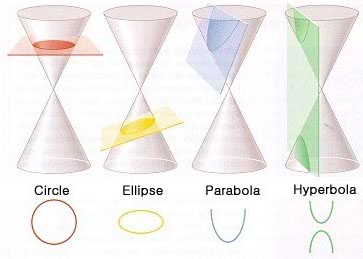
Conics as cuts from a cone The ancient Greeks have already studied the Geometry of how cutting a double cone at different angles produces either a circle, an ellipse, a parabola or an hyperbola. It is also possible to get other shapes as special cases, e.g. can you cut the cones to get a point or a straight line? The word “conic” is derived from the word “cone”. The origin of our words "hyperbola", "ellipse" and "parabola" also come from the Greek study of the conics:

• Parabola, meaning “besides”, when the cut is made parallel to the side of the cone, or at an angle equal to the side angle of the cone (think of para-medic, …)
• Hyperbola, meaning “throwing beyond”, when the cut is made at an angle greater than the parallel angle (think of hypermarket, hyper active, …)
• Ellipse, meaning "falling short", when the cut is made at an angle less than the parallel angle.

Conics interpreted algebraically
Many centuries later it was discovered that the same curves that are produced geometrically by cutting a cone, can also be produced purely algebraically as solutions of the general quadratic equation

ax² + bxy + cy² + dx + ey + f = 0         

As a quick example, open the Quadratic Equations applet below. Then click (lean on) the slider to run the values of a from -5 to 5.
Can you see that you are reproducing the animated picture at the top of this page?
Do you agree that the hyperbola, parabola, ellipse, circle form a continuum?
For what values of a is the graph a hyperbola, for what values is it a parabola, an ellipse, a circle?

Conics as a locus of points
The conics can be described in a unified manner as the locus of a point P so that the ratio of the distance of P from a fixed point F (called the focus) to its distance from a fixed line d (called the directrix) is a constant e (called the eccentricity).
So, if D is the foot of a line from P perpendicular to the directrix, the point P is on the conic section if and only if PF = e x PD. We also know:

• If e = 0, the conic is a circle.
• If e = 1, the conic is a parabola.
• If e > 1, the conic is a hyperbola.
• If 0 < e < 1, the conic is an ellipse.

As a quick example, open the Conics as locus applet below. Then click (lean on) the slider to run the values of P.x from -2 to 20.
Can you see that you are reproducing the animated picture at the top of this page?
Do you agree that the hyperbola, parabola and ellipse form a continuum?
For what values of e is the graph a hyperbola, for what values is it a parabola, an ellipse?

The family of conics is, without doubt, the most important set of curves that Geometry offers the sciences. For example, the reflection properties of the conics are highly useful in Optics, and the shape of orbits of objects around the sun are conics.