3.3
The reflective property of the parabola
Let’s investigate how
a parabola can be drawn through a paper-folding activity that you can
use in class.
Take an A4 piece
of paper and put a dot on it near one edge. Now fold that closest edge
so that it touches the point. Do this about 20 times, unfolding the paper
after each fold and then using a new point on the edge, as shown below:

You should begin to
see your parabola appearing on your paper … Can you explain why
it is a parabola?
You should see that
you form a sequence of isosceles triangles, thus defining a variable point
P(x,
y)
equidistant from two points. Your folds or lines are the altitudes of
these triangles, and are tangent lines to the parabola, forming an “envelope”
around the parabola. To better understand this, open the Folded rectangle
applet below and animate the situation. Also open the Parabola
envelope applet to see what it looks like if all the tangents are
already drawn.
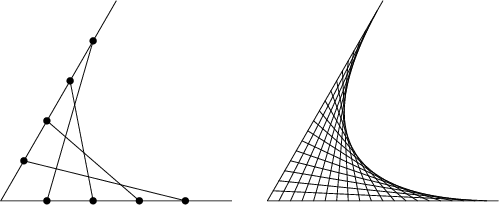
Here is another way
to produce a parabola: Draw two intersecting lines segment and then connect
opposite points on the two lines, as shown below. Can you explain why
it forms a parabola?
|
Open the Tangent applet: 
L is any
tangent to a parabola. The perpendicular from the focus on
the tangent meets the tangent at
P(x,
y).
Find the locus of P.
In the
applet, as the variable point D (x
= a) moves along the directrix, the corresponding variable
tangent to the parabola at x
= a is drawn, as well as the perpendicular from the focus
F onto the tangent. You can drag or animate control D to visualise
the situation.
Can you
prove or explain the general result geometrically?
|
|
|
Given
the point A(-1, -5), find the equation of the tangent(s) from
this point to the parabola y
= x2.
|
|
|