12.
Exponential fit
Let’s now look
at the linearisation of data leading to an exponential model. Open the
Scatterplot applet below and load Example 1.

Example 1
Plotting 10^X vs. Y gives a straight line Y = 0,2X. So:
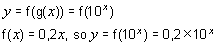
Alternatively, we can use logs.
Note: The only log notation recognised by the applet is log10(Y),
log2(Y) and ln(Y), i.e. loge Y.
Plotting X vs. log10(Y)
gives a straight line log10(Y) = X – 0,6989688
Plotting X vs. log2(Y) gives a straight line log2(Y) = 3,32192641X
– 2.321924
Plotting X vs. ln(Y) gives a straight line loge(Y) = 2,30258393X
– 1,6094351
Let’s now see
how we can deduce the exponential equations from these straight lines:
Now find the equations
of Examples 2 and 3 in the applet through linearisation …
Make sure you reset the plots to X vs. Y after each example.
Check your formulae against the data in the tables. Then click the button
below to check your answers.
Now open the Exponential
Excel tool below and use Excel’s Trendline to fit an exponential
model to each of examples 1, 2 and 3, and compare the results with those
obtained above through linearisation.
 |
 |
|
You
accidentally inhaled some poisonous fumes. Six hours
later, you see a doctor. From a blood sample, she determines
that the poison concentration is 0,00267 mg poison per
cubic centimetre blood, and admits you to the hospital
for observation. The results of blood tests during the
next 36 hours are shown in the table.
|
You
are worried, because medical information says that if
the poison concentration was ever as high as 0,010 mg/cm3,
you could have serious tissue damage. Is there such
a possibility?
The doctor tells you that
you may return to work only when the poison concentration
has dropped to below 0,00010 mg/cm3. When will you be able
to return to work?
The biological
half-life of the poison is the time it takes to drop
to half of its present value. Find the biological half-life
of this poison.
If it
were you that inhaled the poison, you will agree
that it is very important to choose the correct model so that
you can trust it’s predictions! What kind of function
will model this situation?
|
Time
(t
h) |
Concentration
(C
mg/cm3) |
6 |
0,00267 |
10 |
0,00205 |
14 |
0,00157 |
18 |
0,00121 |
22 |
0,00093 |
26 |
0,00071 |
30 |
0,00054 |
34 |
0,00042 |
38 |
0,00032 |
42 |
0,00025 |
|
Use the Excel Poison tool below to try a polynomial, a power
and an exponential fit and discuss the merits of each model.
Also check the linearisation of the data using Scatterplot
(find Poison in the drop-down list). Try to deduce
the regression equation from the linearisation.
There is some feedback in the Excel file, and you can click
below for a further brief discussion:

|
|
Time
(min) |
Temp
(°C) |
0 |
83 |
5 |
76,5 |
8 |
70,5 |
11 |
65 |
15 |
61 |
18 |
57,5 |
24 |
52,5 |
25 |
51 |
30 |
47,5 |
34 |
45 |
38 |
43 |
42 |
41 |
45 |
39,5 |
50 |
38 |
|
The
science class made an experiment to study the rate of
cooling of a cup of hot coffee. They measured the temperature
of the coffee every few minutes and recorded the information
in the table. What algebraic function will model the
situation?
Use
two methods:
-
Use Excel's Trendline in the Excel Coffee sheet to try a
linear, a quadratic, a cubic, an exponential model.
Which one is best? Why do you say so?
Which model is best at predicting the temperature
of the coffee after 100 minutes?

- Use the Scatterplot applet – load the Coffee data,
linearise the data and deduce the equation of the
appropriate model. Compare the equation with the one
you found in Excel.

|
Click
here for some comments: 
|
|
|
Time
(days) |
Amount
(mg) |
0 |
100 |
50 |
76 |
100 |
62 |
150 |
47 |
200 |
37 |
250 |
29 |
300 |
21 |
350 |
17 |
|
A
radioactive element is one that is unstable and decays
into other more stable elements. The table shows the
amounts of Polonium 210, a radioactive element, at times
recorded every 50 days.
The
half-life of a radioactive substance is the
time it takes to drop to half of its present value.
This is an important concept describing the rate
of change of the decay. We can see from the table
that the half life is just less than 150 days, but let’s
find it more exactly. Let’s do it in two ways:
|
| |
- Use
the Scatterplot applet – load the Polonium
data, linearise the data, deduce the equation of the
exponential model, and use the model to calculate
the half-life.
|
|
- Use
the Excel Polonium worksheet to fit an exponential
regression model and use it to calculate the half-life.
|
|
| Click
the Discussion button for some comments: |
|
|
|
|