UNIVERSITEIT VAN STELLENBOSCH
FAKULTEIT OPVOEDKUNDE
DEPARTEMENT DIDAKTIEK
VAKDIDAKTIEK WISKUNDE 174
SEPTEMBER-TOETS 2004

TYD: 2 uur
PUNTE: 150

Eksaminator:
Mnr. A.I. Olivier

Let op:
Die vraestel is ontwerp vir gebruik met Internet Explorer.
Gebruik enige beskikbare tegnologie soos benodig, bv. die MWSnap program en Excel op die netwerk.
Antwoorde moet as 'n Word-dokument voltooi word en as "JouVanNaam.doc" voor 18:30 ge-epos word aan
Save die dokument ook op die netwerk.
Beantwoord al die vrae.

Vraag 1 Vraag 2 Vraag 3 Vraag 4

VRAAG 1
In any parallelogram PQRS, the sum of the squares of the diagonals is equal to the sum of the squares of the sides, i.e.

PR2 + QS2 = PQ2 + QR2 + RS2 + SP2

You can confirm the result numerically in the applet.

Sorry, this page requires a Java-compatible web browser.
  1. Show that in the special case when PQRS is a rectangle, the result follows directly from the theorem of Pythagoras.
  2. Give a general geometric or trigonometric proof.
  3. Give a general coordinate proof.
    Explain why your proof is general.

(30)
Vraag 1 Vraag 2 Vraag 3 Vraag 4

VRAAG 2

Hier is 'n stukkie teks uit Eenheid 20 oor Regressie:

 x
 y
0
5
3
6,5
6
8
9
9,5
12
11
15
12,5
18
14
30
?

Here is a table and scatterplot of an abstract relationship between two variables x and y.
Can you find the algebraic relationship between x and y from the table? Can you predict y(30)?

In the applet, click the sliders, or type values, to change the parameters a and b so that the line y = ax + b goes through all the points (to reset, click “init”).

This process of fitting a graph on given data is called curve fitting or regression.

You should find that the function y = 0,5x + 5 exactly “fits” all the data pairs, that the line passes exactly through all six points, and that y(30) can be confidently predicted as 0,5x30 + 5 = 20.

Maar Lara sê dat y = 0,5x + 4,9 beter pas ("fit"), "want die lyn gaan beter deur die middel van die punte."
Lewer kommentaar!

(30)
Vraag 1 Vraag 2 Vraag 3 Vraag 4

VRAAG 3

Die tabel toon die gemiddelde maandelikse (x = 1, 2, … is Jan, Feb, …) temperatuur (y °C) in Kaapstad. Watter funksie kan die temperatuur modelleer?

  1. Modelleer the data met 'n polinoomfunksie. (Jy kan jou TI-82 sakrekenaar of hierdie Excel-sigblad of enige ander pakket gebruik.)
    Hoe goeie model is dit?

  2. Modelleer die Kaapstad temperatuur met 'n trigonometriese funksie. (Jy kan hierdie Excel-sigblad of enige ander pakket gebruik.)

    Write down the domain and range, amplitude, period and phase for the trigonometric model.
    What physical meanings can you give to these quantities in the context of Cape Town temperature?
    How can these meanings help to calculate the parameters algebraically? Calculate the values of the parameters algebraically!
Maand (x)
Temp (y °C)
1
21
2
21,2
3
20
4
17,4
5
15,1
6
13,3
7
12,5
8
13
9
14,3
10
16,2
11
18,2
12
19,9

(60)
Vraag 1 Vraag 2 Vraag 3 Vraag 4

VRAAG 4

Gebruik jou TI-82 grafiese sakrekenaar (of enige ander program) om die snypunte van die volgende twee funksies te vind, akkuraat tot twee desimale syfers. Beskryf kortliks jou metode.

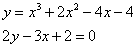(30)
Kliek hier vir toetsantwoorde

Vraag 1 Vraag 2 Vraag 3 Vraag 4