Frames:

6. Inclination of a line


Some aeroplanes have the ability to climb at an unusually large angle. They climb 12 m vertically for every 15 m they move horizontally.

This allows these planes to take off on very short runways. Planes that are capable of doing this are called VSTOL (Vertical short take off and landing).

Here the path of the plane is represented on a coordinate system.
  1. Calculate the gradient of the path of the plane.
  2. Calculate the inclination of the path of the plane.

Click here for the solution:

Calculate the inclination of the line 2x + 5y – 10 = 0.

Click here for the solution:  


Open the Inclination Applet:  

Drag points P and Q to different positions ....
Interpret the inclination (angle with X-axis) shown by the applet.
Use the applet to check your answers for the two activities above.
Make connections between the inclination, the gradient and the equation.

What happens at an inclination of 90° ?
How is the inclination different from the concept of angle in trigonometry? Why is that?

Find the angle between the two lines in Activities 12 and 13, i.e. the angle between 2x – 5y = 0
and 2x + 5y – 10 = 0.

Click here for the solution:    

Develop a formula for finding the angle between any two lines with gradients m1 and m2 respectively.

Click here for the solution:   

A typical mindset of the mathematician is always to look for opportunities to generalise or specialise. So what is the special case when the two lines are perpendicular?

Use the formula 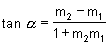to prove the two converse theorems:
1. If two lines are perpendicular, then m1 ´ m2 = -1.
2. If m1 ´ m2 = -1, then the two lines are perpendicular.

Click here for a solution:   

What if the lines are parallel? Use the formula to prove the two converse theorems:
1. If two lines are parallel, then m1 = m2.
2. If m1 = m2, then the two lines are parallel.

Click here for the solution:   

Respond to this question by a learner:

Click here for a discussion: