5.
Loci that are lines
Let’s now look at one
of the simplest loci, namely straight lines.
Definition of a straight line in Analytical Geometry
A line is straight
if it has a constant gradient, i.e. if the gradients between any
two points on the line are equal. Actually,
there are two converse theorems:
- If the gradients
between any two points on the locus are equal, then the locus is a straight
line.
- If the locus is
a straight line, then the gradients between any two points on the locus
are equal.
The following two activities
look at these two theorems.
|
Open the Straight applet: 
The applet opens with a straight line with equation y
= mx
– 2. Drag points P and Q along the line (or click the sliders) and convince yourself that the gradients
between any two points are equal. Then change the gradient (click
the m slider) and check again!
Can you explain why
the gradients are equal? |
|
|
Open the Zigzag applet: 
The applet
shows points P, Q and R not in a straight line. Drag
point Q (or click the sliders) to several positions so
that PQR is a straight line. What can you deduce about the
gradients when PQR is straight and when it is not straight?
Note: This provides
us with a useful strategy to use Analytical Geometry to prove
that points lie in a straight line (are collinear). |
|
Let’s now look
at two other important converse theorems:
- If a locus is decribed by a
linear equation y
= mx + c, then the graph of the locus is a straight line.
- If the graph of a locus is a straight line, then its algebraic equation is linear, i.e. y
= mx + c.
Let's prove the first
theorem. Let (x1, y1)
and (x2, y2)
be any specific solutions of the linear equation
y = mx
+ c. This means that they satisfy the equation, so:
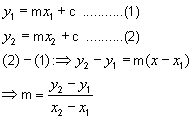
This means that for any two points on the graph of y
= mx
+ c, the gradient is m, i.e. the gradients are everywhere equal (constant).
So, according to our definition, the graph is a straight line.
In the next activity we investigate the second theorem above, namely if
a graph is a straight line, then its equation is linear. You will see that the form of the equation depends on the available information.
|
In each
of the following cases, deduce the equation of the straight
line for the given information. Reflect on the connections
between the information and the equations, e.g. interpret
what graphical meanings can be given to the parameters (i.e.
m, c, x1,
y2,
etc.). Click on the buttons for some discussion.
Find the
equation of the straight line:
| 1.
passing through the origin and through the point (x1,
y1) |
|
| 2.
passing through the point (x1,
y1)
with a gradient of m |
|
| 3.
with y-intercept
c and a gradient of m |
|
| 4.
passing through the two point Q(x1,
y1)
and R(x2,
y2) |
|
| 5.
with x-intercept
a and y-intercept
b. |
|
|
|
| |
The
applet illustrates a most surprising geometric result,
said to have been discovered by Pappus of Alexandria in
the fourth century AD.
Three
points A, B, C and A', B', C', are marked on each of
two lines and then joined as shown. What can you say
about the three points X, Y and Z where the joining
lines intersect?
Manipulate
the applet to form a conjecture and then verify or prove
your conjecture.
|
|
|
|