Frames:

4. The general circle

Let's start with this problem:

We have found that the locus of points equidistant from two points is a line — the perpendicular bisector of the line segment joining the two points.

Another way of expressing “equidistant”, is to say that if the two given points are A and B, and P is a point on the locus, then AP = PB.

A typical mathematical attitude is to generalise results. So the mathematician asks: “What if it is not AP = 1 x PB, but AP = 2 x PB, or AP = 3 x PB, or …“

Given the points A(0, 0) and B(4, 0), find the locus of points P such that AP = 2PB.

Click here for the answer: 

The equation of the locus in Activity 9A is 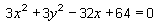. This presents us with a new problem: What type of curve (a line, a parabola, a circle, …) is described by this equation? Any idea?

We can offer the following connection. Look what happens if we expand and simplify the standard form of the equation of a circle, e.g. :

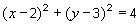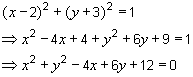
So such equations arise from the standard form of the equation of a circle. So if we start with the equation and work backwards, we can transform such equations to the standard form of a circle:

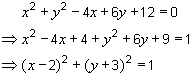
Return to the equation 3x2 + 3y2 - 32x + 64 = 0 for the locus AP = 2 x PB in Activity 9A.
Deduce what kind of a curve it is.

Click here for the answer: 


The general form of the equation of the circle with centre at point (a, b) and radius r is:

x2 + y2 + dx + ey + f = 0

You may wonder why we are using the symbols d, e and f. One answer is that this general circle quadratic equation is a special case of the general conic quadratic equation (see Unit 14)
ax2 + bxy + cy2 + dx + ey + f = 0

But we are not consistant in our use of symbols, e.g. we write the general linear equation as
ax + by + c = 0

Let’s generalise: Given the points A(0, 0) and any point B(a, 0), find the locus of points P such that
AP = 2PB.

Click here for a discussion:  

Let’s generalise: Given the points A(0, 0) and B(4, 0), find the locus of points P such that AP = kPB.

Click here for a discussion:  


Our results are still very special! What if the points are not on the X-axis?
Let’s look at a simple case, say A(0, 0) and B(3, 5) and find the locus of points so that AP = 2PB.

Click here for a discussion:  

Prove that in the general case, for points A(0, 0) and B(a, b), the locus of all points P such that
AP = 2PB is a circle with centre on the line AB. Formulate and prove any other conjectures.

Click here for a discussion:  

We now have the interesting situation:
The locus of P so that AP = 1 x PB is a straight line.
The locus of P so that AP = 2 x PB is a circle.

What would you conjecture is the locus of P such that AP = 3 x PB? Prove it!
Test your conjecture by taking the special case A(0, 0) and B(4, 0).


Open the Apollonius circles applet:  

The applet draws the family of curves for different values of k.
Click (lean on) the slider to run through the values of k from 0,2 to 2.
Beautiful pattern, is it not?

These are called Apollonius circles, named after Apollonius of Perga (about 262-190 BCE), who first investigated loci of the form AP = kPB.


Analyse and draw the graph of x2+ y2 – 6x + 2y + k = 0 for different values of k.

Click here for a discussion:  

It is evident that every equation in standard form can be reduced to the general form by multiplying out the brackets, e.g.

Is the converse true, i.e. can every equation in general form be reduced to standard form, e.g.
  1. Draw the graphs of the following equations by writing them in standard form by completing squares:
  2. In general, when is the general equation x2 + y2 + dx + ey + f = 0 a circle, and when not?
Click here for a discussion:  

Note: You will need to complete the square in many activities in this and the following unit. If you feel you need to practice your skill, click on the Complete square button: