Frames:

The divine proportion

"Geometry has two great treasures: one is the theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold; the second we may name a precious jewel."
Johannes Kepler (1571-1630)		  

Euclid (300 BCE) explains the meaning of "extreme and mean ratio":

“A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.”

Kepler called this the Divine Proportion, but it is today also known as the golden number or golden ratio, golden section, or golden mean. Let’s investigate …

In the applet, point P on the segment AB determines three lengths: the whole, AB, and two parts, AP and PB. Drag point P to find the extreme ratio AB:AP (the whole to the greater) and the mean ratio AP:PB (the greater to the lesser) when

  1. P is the midpoint of AB.
  2. P is a third of the way along AB.
  3. P is a three-quarters of the way along AB.
  4. Can AB:AP = AP:PB?

You should find that the two ratios are always different, except for the one unique value, when
AB:APD = AP:PB » 1,618. This is called the golden ratio! The Greek symbol Phi — f — pronounced “fee” is used for the golden ratio.

Since ancient Greek times, the golden ratio has been considered to be visually appealing. Used in art and architecture, e.g. the famous Greek temple, the Parthenon, is said to have been build using the golden ratio. This ratio does not only appear in art and architecture, but also in natural structures all around us. Because it so often unexpectedly appears in so many different contexts, it is often viewed as “magic” and surrounded with mysticism.

We will dispel any magic and mysticism by showing that the golden ratio is generated by a very specific structure — and that is part of the power of mathematics, that the same structure in very different contexts can be solved with the same mathematics!

The definition of the golden ratio is

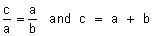
Euclid in 300 BCE showed how to construct the Golden Proportion with compass and ruler only. Descartes showed that if you can construct it, you can calculate it. So lets first calculate it ...

Use the definition of f, it is AB:AP = AP:PB to deduce the numerical value of f.

Click here for the answer:

Open the golden section construction applet:  

Note: section is another word for cut — recall also the conic sections in Unit 14 …

Check this construction in the applet:

  1. Draw segment AB and find its midpoint M.
  2. Draw a perpendicular at B and then a circle B with radius BM cutting the perpendicular at O. Draw AO.
  3. Draw circle O with radius OB to cut AO in C.
  4. Draw circle A with radius AC to cut AB in P.
Then P is the point dividing AB in the golden ratio.
In the applet, drag B to show that the construction and the value of f is independent of the length of AB.
Now prove that the construction gives 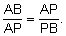Deduce the value of the golden section from the construction.