|
From a
mathematical point of view, the interest in the golden rectangle
is not so much because its dimensions are pleasing to the
eye, but in the fact that a golden rectangle can be partitioned
into a square and a new rectangle, which is again a golden
rectangle, similar to the original. And this process can be
continued to infinity! Formulated differently: the golden
rectangle has the property that when a square is removed from
it, a smaller similar rectangle remains. Thus a smaller
square can be removed from it, and this can be continued …
Open the
Ad Infinitum applet below. In
the applet, click on Rectangle 1, etc, to see the sequence
of successive golden rectangles.
If the dimensions of Rectangle 1 is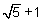 by 2, prove that the 8 rectangles shown in the applet
are all golden rectangles, by finding the dimensions
of each rectangle and showing that the ratio of the longer
side to the shorter side is f.
by 2, prove that the 8 rectangles shown in the applet
are all golden rectangles, by finding the dimensions
of each rectangle and showing that the ratio of the longer
side to the shorter side is f.
Write
down the lengths of the longer sides of the 8 rectangles as
a sequence. What kind of sequence is it? Prove it!
Write down the general term Tn for the sequence,
and check your formula by using it to calculate the first
four terms of the sequence.
Write
down the lengths of the shorter sides of the 8 rectangles
as a sequence. What kind of sequence is it? Prove it!
|