Two triangles are similar iff ...

Definition of similar triangles
Similar triangles are a special case of similar polygons, so one should prove triangles similar in exactly the same way as for polygons in general.

However, the interesting thing is that in the special case of triangles (and this applies only to triangles), it is not necessary to prove both conditions, because it can be proved that the one implies the other.

Unless our learners understand the general conditions for similar polygons, they will not appreciate the beauty, simplicity and the usefulness of the two triangle similarity theorems,i.e.

• equal angles Þ proportional sides, and its converse
• equal angles Ü proportional sides

In his section we offer you some experiences of these important concepts, and we deduce a third test for similarity of triangles, which is not in the school curriculum (why not!?).

Are equiangular triangles proportional?
We have shown that equiangular polygons do not necessarily have proportional sides, so are not necessarily similar. Let’s now investigate this question for triangles.

Open the Triangle similarity applet:

In the applet, the figures were constructed by drawing parallel lines, so all the corresponding angles of the triangles are equal. Now manipulate the figures and note the measures. Can you conclude that the sides of the triangles are proportional? Can you explain it?

Sufficient conditions If two pairs of sides of two triangles are proportional, can we conclude that the two triangles are similar? This applet illustrates the situation: although the given sides are in proportion, it should be clear that we cannot conclude that triangles ABC and A¢B¢C¢ have the same shape – for example, C¢ can be anywhere on the circle and the sides will still be proportional!

So two sides in proportion is not sufficient information for similarity. What additional information is needed to fix the triangles so that they will be similar?

Do you agree that we need either

• the third side, i.e. if all three pairs of sides of two triangles are proportional, then the triangles are similar, or
• the included angle, i.e. if two pairs of sides of two triangles are in proportion, and the included angles are equal, then the triangles are similar.

In addition we know

• If two triangles are equiangular (i.e. if two angles in the two triangles are equal), then the triangles are similar.

Enlargement
Open the Enlargement applet:

The applet shows how to construct an enlargement of a polygon. A and A¢ are points on ray OA. The two quadrilaterals are then constructed by drawing parallel lines between the rays, so they are equiangular.

You can drag points A, B, C and D to change the shape of the quadrilaterals. You can drag A¢ to change the size of the enlargement (OA¢:OA is called the scale factor and O is called the centre of enlargement). Interact with the applet and note the ratio of the sides for different shapes and different sizes. When is the scale factor bigger than 1, equal to 1, les than 1? Try moving point O inside ABCD …

Do you agree that the sides of the equiangular quadrilaterals are also proportional, and that ABCD and
A¢B¢C¢D¢ are therefore similar? Can you supply an explanation or proof? How and why is this different from the non-similar equiangular polygons on the previous page?

Can you prove the converse: If we construct the quadrilaterals so that

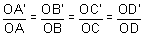
can you prove that the corresponding sides are then parallel, and therefore that the quadrilaterals are equiangular?