Triangle similarity theorems

We can formalise all the previous conditions that we have encountered into formal proofs for similar triangles.

Equiangular Theorem
If the corresponding angles of two triangles are equal, then the corresponding sides are in proportion, and therefore the triangles are similar.

Rather than require our learners to learn the proof for this theorem off by heart, we should encourage them to devise and remember a strategy for proving it. The following animation can help us with our strategy for proving this theorem.

Click here for a reminder of the proof according to our strategy:

Equiangular theorem converse
The converse of the equiangular theorem is:

If the corresponding sides of two triangles are proportional, then the corresponding angles are equal, and therefore the two triangles are similar.

We can devise a similar strategy to prove the theorem.

Included angle theorem:
The third proportionality theorem states:
If two corresponding pairs of sides of two triangles are in proportion and their corresponding included angles are equal, then the triangles are similar.

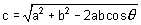
Here is an outline of a proof: If two pairs of sides are proportional, then if the sides of one triangle are a and b, then the corresponding sides of the other triangle will be ka and kb respectively. It is now easy to show that the third sides are also proportional. If the third side of the first triangle is c, then If the third side of the second triangle is d, then

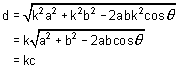
So all three sides are proportional, and by our previous theorem it follows that the two triangles are similar.