4.2
The equation of an ellipse
We want to deduce the Cartesian
equation of the ellipse from its tack-and-string definition. We first
solve a special case – carefully note the process, which we will
then use in the general case.
|
Let P(x,
y)
be any point on the ellipse with foci A(-3, 0) and B(3, 0)
so that AP + PB = 10.
Deduce the Cartesian equation of the
ellipse from this condition.

|
|
| The
ellipse is conventionally placed with its centre at the origin of
the coordinate system, with foci at (-c, 0) and (c, 0). So the
foci are 2c apart. The width of the ellipse is taken as 2a, which
means it has x-intercepts
at a and -a. The height is taken as 2b, which means it has y-intercepts
at b and -b. The distance 2a is called the major axis
and a the semi-major axis. Likewise 2b is called the minor
axis and b the semi-minor axis. |
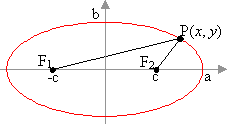 |
By definition, F1P + F2P is a
constant for any point P on the ellipse. But what is this constant?
When P is at a, we have F1P
+ F2P = 2c + 2(a – c) = 2a.
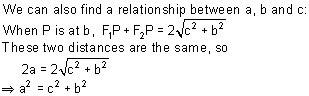
|
Use the
above information to deduce the Cartesian equation of the
ellipse in terms of the parameters a and b.

|
|
The standard form of the equation of the ellipse with centre (0, 0), major axis 2a and minor axis 2b is
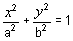 . If, instead
of being centred at (0, 0), the centre of the ellipse is at
(h, k), the equation is
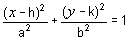 . |
|
|
Open the Ellipse graph applet below, drawing graphs of 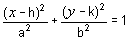

In the applet, vary the parameters h, k, a and b by dragging the centre M or
clicking the sliders.
Formulate a theory of how they influence the graph ...
|
|
|
Draw the
graphs of the following equations by writing them in standard
form by completing squares:
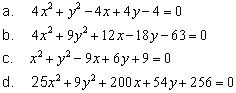
Click
here for the answer: 
|
|
|