MN is perpendicular to the X-axis, with M a point on the circle x2 + y2 = 16 and N on the X-axis. What is the locus of P, the midpoint of ordinate MN, for all points M on the circle? In the applet, drag or animate point M. Do you agree that the locus is an ellipse? But how do we prove it is an ellipse, how do we describe the ellipse and what is its equation? Click for a discussion:

Sorry, this page requires a Java-compatible web browser.

Let us now generalise: In the applet above, change the radius by dragging r, clear the traces and animate again. Can you predict the equation of the ellipse?
Find the equation in the general case when the radius is r.

Click for a discussion:  

Open the Ellipse locus applet and move it so that you can see this text and work in the applet.

Let’s now generalise further: What if the centre of the circle is not at the origin? In the applet the centre of the circle is at 0(5, 3), with a radius of 4. Find the equation of the locus of P using Analytical Geometry methods.

Open the Ellipse locus 2 applet.

Let’s now generalise further: What if P is not the midpoint of MN, but any point on MN?
This means that the ratio MN:PN is constant.
First solve the specific problem shown in the applet, i.e. a circle O(5, 3), radius 4, and P such that MN= 3PN.

Then solve the general case for a circle O(h, k) with radius r and P such that MN = mxPN.

Open the Parametric equations applet. Drag or animate point T around the circle. It certainly looks as if the locus of P is an ellipse! Vary a and b and animate again! Can you prove that it is an ellipse?
Tip: Prove it is an ellipse by proving that the equation of the locus is 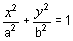.