5.2
The Cartesian equation of the hyperbola
We want to deduce
the Cartesian equation of the hyperbola from its definition, in the
same way we did for the ellipse in section 4.2.
|
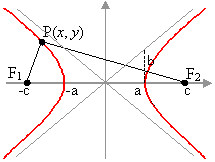
The hyperbola
is conventionally placed with its centre at the origin of the coordinate
system, with foci at (-c, 0) and (c, 0). So the foci are 2c apart.
The hyperbola cuts the X-axis at -a and a.
By definition, F2P –
F1P is a constant for any point P on the hyperbola. But
what is this constant?
When P is at
-a, we have: F2P – F1P = (c + a) – (c –
a) = 2a.
|
 |
|
Use the
above information to deduce the Cartesian equation of the
hyperbola in terms of the parameters a and b.
Click
here for the answer: 
|
|
The standard form of the equation for a hyperbola with semi-major
axis a parallel to the X-axis and semi-minor axis
b parallel to the Y-axis is given by
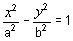
If, instead
of being centred at (0, 0), the centre of the hyperbola is
at (h, k), the equation is
|
|
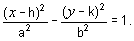
Open the Hyperbola graph applet, drawing graphs of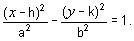 
In the applet, vary the parameters h, k, a and b by dragging the centre M or
clicking the sliders.
Formulate a theory of how they influence the graph ...
|
|
|
Draw the
graphs of the following equations by writing them in standard
form by completing squares:
a.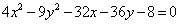 
b.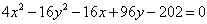 
Click
here for the answer:
|
|
The
tangent to the function xy = 5
at A intersects the Y-axis at C and the X-axis at D.
- Show
that A is the midpoint of CD.
-
Show that OCxOD is constant for the tangent at x
= 1. Also show that
OCxOD is constant for the tangent at
x = 2 and at x
= 5, and in general at any x
= a.
-
Generalise further by proving the results in (a) and
(b) for the tangent at any point x
= a for any hyperbola xy = k.
|
|
|
|
|