3. Tides

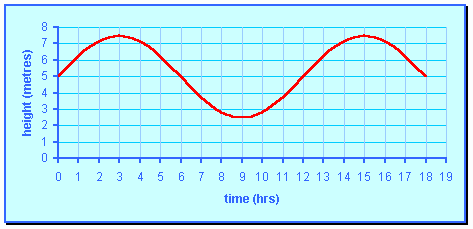
Suppose that the height of the tide, h metres, at a harbour entrance is modelled by the function h = 2.5 sin 30t° + 5 where t is the number of hours after midnight. Study the graph representing the function h = 2.5 sin 30t° + 5 and then answer the questions that follow.

sin 30t° is very confusing! We never write 2x cm + 1 or sinx° . Rather omit the ° !

I am not sure about hrs as the abbreviation of the word hours. Rather write it out, like you wrote out metres.

  1. How many hours after midnight will it be high tide?

    2. Type your answer here.

  2. When will it be high tide again?

    3. Type your answer here.

  3. How many hours does it take from one high tide to the next high tide?

    4. Type your answer here.

  4. What is the approximate height of the tide at high tide?

    5. Type your answer here.

  5. When will the height of the tide be 5 metres?

    6. Type your answer here.

  6. What will the height of the tide be 7 hours after midnight?

    7. Type your answer here.

  7. When will the tide reach this height again?

    8. Type your answer here.

  8. What is the minimum value of this function?

    9. Type your answer here.

  9. What does the minimum value mean in this situation?

    10. Type your answer here.

  10. When does this function reach its minimum value?

    11. Type your answer here.

  11. Use the equation h = 2.5 sin 30t° + 5 to complete the table below Compare the table of values to the graph shown above.

    12. Time (hrs)

    0

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    Height (m)

     

     

     

     

     

     

     

     

     

     

     

     

     

    Time (hrs)

    13

    14

    15

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    Height (m)

     

     

     

     

     

     

     

     

     

     

     

     

     

  12. Describe how the height of the tide is related to time i.e. describe the behaviour of the function h = 2.5 sin 30t° + 5.

    13. Type your answer here.

    Hypertext answer

    The height of the tide increases, reaches a maximum at high tide, decreases until it reaches a minimum at low tide. The tide the increases again and the pattern continues over and over again. This is an example of a periodic function.

     

    Hypertext for periodic

    A periodic function is a function that repeats themselves itself after a certain interval, known as the period.

    This is too loose!
    There is only one function - how can it repeat itself? Meaning - the whole thing, e.g.
    y = sinx is the function, it cannot repeat itself!
    What we mean is that the function values are the same. For example the periodicity of y - sinx lies in the property that sinx = sin(x + 360n), i.e. the function values are equal every 3600.

     

  13. What is the period of the function h = 2.5 sin 30t° + 5?

Type your answer here.

 

RETURN TO PREVIOUS