3. The distance formula

In the sketch, how far is the ball from the basket when the netball player in the free throw releases it?

Using Synthetic Geometry , we can apply the Theorem of Pythagoras in triangle ABC:

In Analytical Geometry, we use an alternate approach: We use a coordinate system to work out the distance between the two points.

Distance in one dimension
Firstly, we need to clarify what “distance” means in a one-dimensional system (i.e. on a number line).

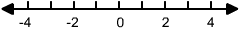
The distance between two points in a one-dimensional coordinate system is defined as the absolute value of the difference between their coordinates. For example, on this number line: Distance between -1 and 3 is 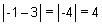Distance between 3 and -1 is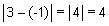

Distance in two dimensions
The diagram below shows how we introduce co-ordinates, use the definition of distance in one dimension and apply the theorem of Pythagorus to deduce a formula for the distance between two points in two dimensions:

Synthetic Geometry	Coordinate Geometry

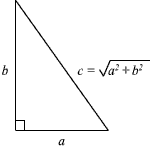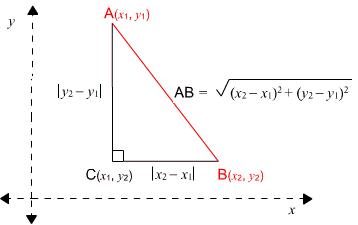Think about the following:

• What happened to the absolute signs in the formula? Should the formula not be


• 
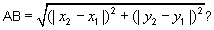
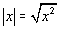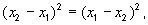• and in other words the order does not matter.
• It is often useful to work with the square of the distance to avoid surds, e.g. AB² = 13 instead of

Let’s now solve the netball problem using Coordinate Geometry. As in all problems, our first task is to decide where to place the origin of the coordinate system. We show below two positions and the corresponding mathematics. Which one do you prefer and why?

The coordinates are A(0, 0) and B(5, 1):

The coordinates are A(0, 2) and B(5, 3):

Triangle ABC has vertices A(3, -2), B(2, 4) and C(9, -1). Prove that the triangle is isosceles.