|
2.3
Introduction to locus
Descartes
was hoping to free geometry from the use of diagrams through the use of
algebraic procedures. He also wished to give meaning to algebraic
operations by interpreting them geometrically. These two ideas are embodied
in the concept of locus.
The two basic problems
of Analytical Geometry are:
- Given the condition
or description of a locus, to find the algebraic formula or equation
of the locus (e.g. the locus of points at a distance of 3 from the point
(0, 0) is given by the equation x2
+ y2
= 9).
- Given an algebraic
equation of a locus, to find its geometric (graphic) representation
or description in words (e.g. the locus of points satisfying the equation
x2
+ y2
= 9 lies on a circle with centre at (0, 0) and a radius of 3).
To this we can add:
Constructing a locus (geometrically), and proving that
the construction satisfies the condition (geometrically and algebraically).
But what is
a locus?
The word locus
is used in mathematics to mean either:
- the set of all points which satisfies a
given condition.
- the path or trajectory traced out by one point which moves in such a way that it always
satisfies a given condition.
The
word locus is derived from the Latin, meaning location or place.
What connections can you make between locus and place and path?
How are the two definitions of locus different, and how are they the same? Can you connect them?
Some examples of loci
Open the Locus applet: 
Click Locus 1, Locus
2, Locus 3 ... How will you describe these loci?
Locus 1 could be the
trajectory (path or orbit) of a planet around the sun.
Locus 2 could be
the path of the moon around the earth, or the path of a stone swung
on a string.
Locus 3 could represent the trajectory of a comet around
the sun. It is not clear from the geometric representation whether the
path is an ellipse (so it is a periodic, like Halley’s comet) or
if it is a parabola or a hyperbola (so the comet passes only once). It
is only through an algebraic description of the path that we can know
its characteristics. |
|
|
Open the Orthocentre applet: 
The applet shows the orthocentre
P
of triangle ABC. If we think of the vertices as variables, then as the vertices move, so will the orthocentre.
But how does it move, what is its locus?
-
The applet opens with Locus 1: Vertex B of triangle ABC moves along the horizontal red line.
Can you visualise
what path P will follow?
Now drag or animate point B …
Surprised? Try to prove that the locus is a parabola and find
its equation.
- Now click Locus 2 and clear traces.
What is now the locus of P as B moves along the red line? Can you prove
it?
- Now click Locus 3 and clear traces.
What is now the locus of P as B moves along the red circle? Can you prove
it?
We will return to
these loci in section 8. |
|
|
Let's
now investigate how Descartes constructed a square root locus ...
Open the Square Root applet and move
it so that you can see this text and work in the applet:
 |
We
have already seen how Descartes showed that 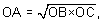 and
if OB = 1, and
if OB = 1, 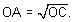 Descartes
conceived of the length OC as a variable x,
thus defining a point P(x,
y) in the coordinate
system. He conceived of point C moving along
the X-axis, and as it moved, P traced out a corresponding
path which was the picture (graph) of Descartes
conceived of the length OC as a variable x,
thus defining a point P(x,
y) in the coordinate
system. He conceived of point C moving along
the X-axis, and as it moved, P traced out a corresponding
path which was the picture (graph) of 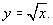 In the applet, drag or animate point C. Check specific
values, e.g. check the result for special cases like
x
= 4 and 9 …
In the applet, drag or animate point C. Check specific
values, e.g. check the result for special cases like
x
= 4 and 9 …
Now
drag point B to change the parameter a, so that OB is
not 1, then drag or animate C – the locus is the
graph of 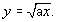 Try
different values of a and describe how a influences
the graph of Try
different values of a and describe how a influences
the graph of 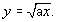
Descartes
could also find the intersections of loci.
In this way he solved the classical Greek problem of
doubling the cube: using only ruler and compasses,
construct the side of a cube that has twice the volume
of a cube with a given side. This proved to be impossible.
But Descartes found the solution by finding the simultaneous
solution of the two equations y
=
x2 and 2x
= y2.
Explain why the intersection is the solution of x3
= 2.
|
|
|
- Given
points A(0, 0) and B(10, 0), find the locus of points C
so that triangle ABC has an area of 20 square units.
- Draw
and describe the locus of points that are two units away
from any point A.
Click
for the solutions:
  |
|
|