|
4.
The midpoint of a line segment
One of the most important
and useful results in Analytical Geometry is the formula for the midpoint
of a line segment, given the coordinates of the endpoints. We know how
to construct the midpoint of a segment in Geometry, so let’s follow
Descartes’s assertion that “if it can be constructed, it can
be calculated”.
Place AB on the
coordinate system and introduce the notation A(x1, y1)
and B(x2, y2)
and M(x, y).
|

|
Notation
By convention we use the notation (x1,
y1)
and (x2,
y2)
to indicate given or fixed points (constants or parameters)
and (x,
y)
to indicate either a moving variable point as we
do when working with loci, or an unknown point as
we have here.
|
|
An intuitive approach
would be to start with the fact that if M is the midpoint of AB, then
AM = MB, and then use the distance formula:

This looks very complicated!
In such cases one can either persevere, or look for an alternate strategy!
Click here to see
this strategy continued. However, we will here develop another approach.
A very useful strategy in Coordinate Geometry is to try to use horizontal and vertical components,
because these can be expressed very simply as the difference between coordinates (distance in one dimension).
Similar triangles is then often a useful entry.
So make the constructions and name the points as shown. Because MC
and BD are vertical, and AD horizontal, we can deduce the coordinates C(x,
y1)
and D(x2,
y1).
|
|
Using the geometry
midpoint theorem or that 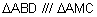 ,
we have ,
we have 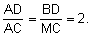 So: So:
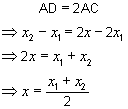 |
and |
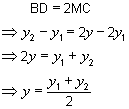 |
|
The coordinates
of the midpoint of a line segment is the average of
the coordinates of the endpoints!
Generalising
The approach of working with the components of the points is very important
and generalisable to all cases involving proportion.
|
Instead
of expressing the midpoint as AM = MB, we could interpret
it as AB = 2AM. Now we can use this idea to find the co-ordinates
of the point M that divides AB so that AB = 3AM, or in general
so that AB = kAM.
- M is
a point on segment AB so that AB:AM = 3:1. If the endpoints
have coordinates A(-1, -2) and B(2, 3), find the coordinates
of M.
- Find
a general formula for the coordinates of a point M on AB
with endpoints A(x1,
y1) and
B(x2,
y2),
so that AB = kAM.
Click
here to see the solution: 
|
|
|