2.
The circle with its centre at the origin
Our problem for this section is:
What
is the locus of points that are equidistant from a fixed point?
|
We
know from our geometric knowledge that the locus is a circle. Now we want to approach the problem using Analytical Geometry and to find the algebraic
equation of the locus (circle).
This
applet visualises the problem: drag or animate point P.
Change
the distance by dragging Q or M, clear any traces and drag P again …
|
|
We
will use two different approaches to solve the problem in the following
two activities.
|
Use
the definition of the distance between two points to find
the locus of points that are equidistant from a fixed point.
For convenience, place the fixed point at the origin of the
coordinate system.
|
|
|
The
co-ordinates of any point P(x,
y)
on the locus is given by the pair of parametric equations:
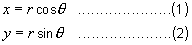
Use these equations to deduce the analytic form of the equation
of the circle.
Click
here for a discussion  |
|
|
Find
the locus of points that are a distance of 3 units from the
origin.
Click
here for the answer:  |
|
|
Six
points, A, B, C and A', B', C', are marked on the circle
x2
+ y2
= 25 and then joined as shown. What can you say about
the three points X, Y and Z where the joining lines intersect?
Manipulate
the applet to form a conjecture and then verify or prove
your conjecture.
Click here for a discussion:
|
|
|
|