The Fibonacci connection
We now
investigate a surprising arithmetic connection to the geometric golden
ratio.
The
Fibonacci-sequence is the sequence 1, 1,
2, 3, 5, 8, 13, 21, 34, …
where T1 = T2 = 1, and Tn
= Tn –2 + Tn
–1 for n > 2, i.e. each term of the sequence
is the sum of the previous two terms.
|
|
|
Use your
calculator, and form a new sequence consisting of the ratio
of successive terms of the Fibonacci sequence, i.e.
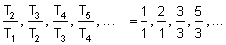
What
do you notice about this sequence? To compare your solution,
click to open the Fibonacci Excel file.
Can you
explain why the ratio of successive numbers yield
the golden ratio?
|
|
|
Open the
animation below to construct an alternative Golden Spiral,
another surprising connection between the Fibonacci sequence
and the golden ratio.
Is this
the same spiral as before?
Write down the
lengths of the longer sides of the constructed rectangles
as a sequence. What kind of sequence is it?
Write down the
lengths of the shorter sides of the constructed rectangles
as a sequence. What kind of sequence is it? |
|
|
The following
shows surprising connections to the golden section. Can you
explain it?
Calculate
each of the following and find its limit:
|
|
To read
more about the golden ratio, see these external
links:
Fibonacci
Numbers in Nature
The
Golden Proportion
Phi:
The Golden Number
|