|
Extension and investigation
Here
are some investigations and problems for yourself, that that you can also
use with your learners to reinforce the concept of similarity and its
applications.
| Golden
triangle and pentagon
Investigate this beautiful figure … Click on the picture to
open the Pentagram applet.
ABCDE is a regular
pentagon, i.e. all its sides and all its angles are equal.
The diagonals are drawn, resulting in a star called a pentagram
and an embedded similar smaller pentagon PQRST. This process can
be continued infinitely …
|
|
- Calculate the relevant
angles in the figure. Name a few congruent and a few similar triangles.
- Click on the Golden
triangle 1 button. Prove that DDAB
is a 36°-72°-72° triangle. Now prove that:
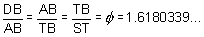
Tip: Put DT = AB = a and TB = b and prove the golden ratio
structure, i.e.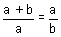 . .
We call DAB a golden triangle. Like the golden rectangle, we can construct
a sequence of golden triangles – show that triangles BAT and TBS
are golden triangles. How many golden triangles can you find in our
pentagon?
- Click on the Golden
triangle 2 button. Prove that DDEC
is a 108°-36°-36° triangle. Now prove that:
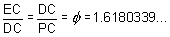
DDEC is also a golden rectangle,
different from DDAB. How many such
golden triangles can you find in our pentagon?
- Click on the Other
ratios button. The many parallel lines lead to similar triangles
and interesting relationships. For convenience, let d1 and
s1 denote the diagonal and side of the first pentagon ABCDE,
and d2 and s2 the diagonal and side of the second
pentagon PQRST, etc. Prove that:
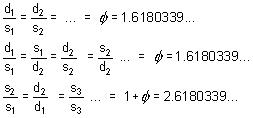
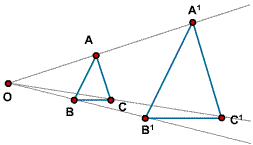
| Properties
of triangles
Click on the
picture to open an applet of similar triangles ABC and A¢B¢C¢.
You can change the shape of the triangles by dragging A, B and C
and change the scale factor by dragging A¢.
Investigate the
relationship between the following properties of the two triangles
and the ratio of the sides of the triangles (the scale factor):
perimeter, area, altitude, median. Prove your conjectures!
|
 |
| Tangents
Click on the
picture to open an applet showing three circles touching internally.
Investigate the ratio of the length of the sides of the triangles
formed by two chords. How is this related to the radii of the circles?
Can you explain or prove your findings?
|
|
| Chords,
secants and tangents
Click on the
picture to open the Chords applet.
- Chords AB
and CD intersect at P inside the circle.
Prove that PA.PD = PB.PC
- Specialise
by checking the nature of the result when:
- P is
the centre of the circle.
- PA =
PB and PC = PD (when AB || CD).
- Generalise
by proving that the relationship in 1 applies also when AD and
BC intersect outside the circle (interchange B and D
in the applet).
- Now specialise by taking the following limiting cases. How does
the result in 1 change?
- Secant PDA becomes a tangent PA to the circle (move A and
D to fall on top of each other).
- Secant PBC also becomes a tangent PB to the circle.
Show that you can deduce that PA = PB.
|
|
|
A
star
In
this applet, three lines are drawn parallel to the sides of DABC.
Drag
the red points ...
Are all the smaller triangles formed similar?
Prove it!
|
|
|