4.4
The ladder locus
|
A ladder stands vertically
against a wall. The foot of the ladder is pulled away from the wall,
from its upright position at A, to its final position at B, when
the ladder lies flat on the ground.
In the applet,
drag the foot of the ladder …
If P is any point on the ladder, what do you think is the
locus of P as the foot of the ladder slides from A to B?
Is the locus different for different positions of P?
Now let’s
check the locus visually using technology! Open the ladder animation:
|
|
|
Now use
Analytical Geometry to deduce or prove your conjecture:
Find the equation and the shape of the curve of the locus
of any point P on the ladder.
Click
here for a discussion:  |
|
|
Activity 16 proved that the ladder locus is an ellipse for any point
P. But did you not think that if P is the midpoint of the ladder the locus
is a circle? Is this not contradictory?
Deduce from the equation of the ellipse locus 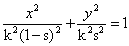 that if P is the midpoint of the ladder, then the locus is a circle.
Click
here for a discussion: |
|
Here is another interesting approach to prove that the locus of the midpoint P of the falling ladder is a circle:
If OP is constant, then, by definition, P lies on circle O with radius OP!
Prove that OP is constant (and find the value of the constant) using:
1. Synthetic Geometry
2. Analytical Geometry
Click
here for a discussion:
|
|
|
|
|
If P is
at either end of the ladder, the locus is a straight line.
Do you agree? Prove that the locus is a straight
line!
Click
here for a discussion: |
|
The
trammel
The mathematics
of the falling ladder is applied in the carpenter's trammel, an
instrument for drawing ellipses. It consists of a cross with two
grooves at right angles to each other, and a beam carrying two pins
(which slide in those grooves), and also the describing pencil.
In this illustration, you can animate the device, or you can drag
the control. You can also drag the red point on the right "ladder"
to change the dimensions of the ellipse.
Can you use the trammel to draw a circle?
Can you use the trammel to draw a straight line? |
|
|